Variational Autoencoder

Introduction

Variational Autoencoder는 GAN 이전에 강력한 생성 모델(generative model)로 유명했기 때문에 알아둬서 나쁜 것이 없지만 수학적으로 다소 복잡한 계산이 많아 쉽게 이해하기 어려워 이해하거나 구현하기 어렵다는 문제가 있죠. 게다가 이름은 분명 Autoencoder인데 우리가 익히 알고 있는 Autoencoder와 특징적인 차이가 있어 더 어렵게 느껴집니다.

본 포스트는 Variational Autoencoders for Collaborative Filtering 논문을 읽으면서 VAE에 대한 복잡한 내용을 쉽게 정리할 필요가 있어 작성하게 되었습니다. 수학적인 부분은 최대한 쉽고 자세하게 작성하였으며, 최대한 유도 가능한 부분은 유도하여 이해를 돕고자 했습니다.

Difference between AE and VAE

우선 Autoencoder의 목적은 원본 데이터 $X$를 다시 재구현하는 과정에서 얻는 잠재 변수(latent feature)를 잘 만드는 것입니다. 이 목적에서 비롯하여 Autoencoder를 차원 축소에 사용하거나 변수 추출에 사용하게 됩니다. 이와 다르게 VAE는 Autoencoder의 구조를 본뜬 생성 모델입니다. 이름에서도 나와있듯이 Autoencoder에 Variational Inference 개념을 도입한 모델이죠. Autoencoder와 VAE는 이름은 비슷하지만 완전히 다른 개념을 갖고 있습니다.

:bulb: Autoencoder와 VAE의 차이

• Autoencoder (AE)
  • 입력값을 잠재 공간(latent space)로 맵핑하여 압축된 값을 생성하기 위해 사용함
  • 잠재 변수들이 regularized 상태가 아님
  • 임의의 잠재 변수를 선택하면 의미 없는 결과를 반환함
  • 잠재 변수들이 불연속적이며 결정론적(deterministic)인 값
• Variational Autoencoder (VAE)
  • 잠재 변수들이 평균과 분산의 형태로 구성됨
  • 잠재 변수들이 연속적임
  • 잠재 변수로부터 뽑은 임의의 값들이 디코더에서 유의미한 결과를 생성함
  • 디코더에 사용되는 입력값은 인코더의 결과값로부터 얻은 평균/분산을 따르는 가우시안 분포로부터 샘플링한 stochastic한 값들임
  • Regularized 상태의 잠재 변수를 가짐

Variational Autoencoder

Intuitions

어떤 학습 데이터 $\mathbf{x}$ 가 관측되지 않은 잠재 변수인 $\mathbf{z}$ 로부터 생성되었다고 가정하겠습니다. 여기서 잠재 변수 $\mathbf{z}$ 의 확률밀도함수를 파라미터 $\theta^\ast$ 에 대해 $p_{\theta^\ast}(z)$ 라고 할 때 생성된 학습 데이터 $\mathbf{x}$ 는 조건부 확률 분포 $p_{\theta^\ast} (x \mid z)$ 로부터 샘플링되었다고 할 수 있습니다. 우리는 여기서 파라미터 $\theta^\ast$ 를 추정하는 것이 목표입니다.

이때 $p_{\theta^\ast}(z)$ 는 사전 분포(prior distribution)가 되는데 이 분포를 간단하게 가우시안 분포로 가정하겠습니다. 그러나 조건부 확률 분포 $p_{\theta^\ast} (x \mid z)$ 는 매우 복잡한 형태가 됩니다. 따라서 이 부분은 신경망으로 나타내고자 하며 $\mathbf{z}$ 로부터 $\mathbf{x}$ 를 생성하는 이 부분이 VAE의 디코더가 됩니다. 이와 같은 생성 모델을 학습하여 파라미터를 추정하는 것은 일반적으로 학습 데이터의 우도(likelihood)를 최대화하는 것과 같습니다. 따라서 다음의 marginal likelihood를 계산해야 합니다.

\[p_\theta(x) = \int p_\theta(z) \; p_\theta(x\mid z) \; dz \notag\]

하지만 이 식을 계산하는 쉽지 않습니다. $p_\theta(z)$는 가우시안 분포로 가정하고 $p_\theta(x\mid z)$는 신경망으로 대체하기 때문에 각각은 계산이 어렵지 않습니다. 하지만 $z$에 대해서 $p_\theta(x\mid z)$를 적분하는 것이 불가능합니다. 그뿐만 아니라 $z$의 특성을 추론하기 위해 계산해야 하는 posterior density도 계산할 수 없습니다.

\[p_\theta(z \mid x) = \frac{p_\theta(x \mid z) \; p_\theta(z)}{p_\theta(x)} \notag\]

이 posterior density는 $x$로부터 $z$를 찾아내는 일종의 인코더가 되는데요. 분모인 $p_\theta(x)$를 계산할 수 없으므로 우리는 인코더에 대한 학습을 할 수 없습니다. 이같은 직접적으로 계산할 수 없는 상황을 intractable하다고 하는데요. Intractable한 적분을 직접 하는 대신 그 적분을 근사(approximate)하여 문제를 해결하는 방식을 변분 베이즈 방법(variational bayesian methods)라고 합니다. 변분 추론(Variational inference)라고도 하죠. 우리는 이 방법을 이용하여 인코더 $p_\theta(z \mid x)$를 직접 계산하는 대신 이에 계산 가능하며(tractable) 인코더에 근사하는 $q_\phi(z \mid x)$를 정의하여 문제를 해결하고자 합니다. 인코더와 디코더의 구조는 다음과 같습니다.

Figure 1. The structure of encoder and decoder for VAE.

Mathematical Motivation

우리는 지금까지 여러 방법을 이용해 인코더와 디코더를 정의했습니다. 이제 위에서 논의했던 학습 데이터의 우도를 최대화하는 것에 집중해야 합니다. 학습 데이터의 우도는 다음과 같이 다시 쓸 수 있습니다.

\[\begin{align*} \log p_\theta(x) &= \mathbb{E}_{z \sim q_\phi(z \mid x)} \left[ \log p_\theta(x) \right] \tag{1} \\ &= \mathbb{E}_z \left[ \log \frac{p_\theta(x \mid z) \; p_\theta(z)}{p_\theta(z \mid x)} \right] \tag{2} \\ &= \mathbb{E}_z \left[ \log \frac{p_\theta(x \mid z) \; p_\theta(z)}{p_\theta(z \mid x)} \frac{q_\phi(z \mid x)}{q_\phi(z \mid x)} \right] \tag{3} \\ &= \mathbb{E}_z \left[ \log p_\theta(x \mid z) \right] - \mathbb{E}_z \left[ \log \frac{q_\phi(z \mid x)}{p_\theta(z)} \right] + \mathbb{E}_z \left[ \log \frac{q_\phi(z \mid x)} {p_\theta(z \mid x)} \right] \tag{4} \\ &= \underbrace{\mathbb{E}_z \left[ \log p_\theta(x \mid z) \right]}_{(5-1)} - \underbrace{D_\text{KL} \left( q_\phi(z \mid x) \ \| \ p_\theta(z) \right)}_{(5-2)} + \underbrace{D_\text{KL} \left( q_\phi(z \mid x) \ \| \ p_\theta(z \mid x) \right)}_{(5-3)} \tag{5} \end{align*}\]

• (1) : $p_\theta(x)$는 $z$에 의존하지 않기 때문에 기댓값(expectation)으로 나타낼 수 있습니다.
• (2) : 베이즈 정리에 의해서 유도됩니다.
• (3) ~ (4) : 로그 안에 상수를 곱한 다음 식을 전개합니다.
• (5) : 두 분포를 나누어 로그를 취한 것의 기댓값은 Kullback-Leibler Divergence로 나타낼 수 있습니다.
  • (5-1) : 디코더의 likelihood에 대한 기댓값입니다. 이 값은 계산 가능한 값입니다.
  • (5-2) : 인코더의 근사 분포와 사전 분포의 KL Divergence입니다. 인코더의 근사 분포는 기본적으로 계산 가능하며 사전 분포 역시 가우시안 분포이므로 계산 가능합니다.
  • (5-3) : $p_\theta(z \mid x)$가 계산 불가능하기 때문에 이 항 역시 계산 불가능합니다.

결론부터 말하자면 학습 데이터의 우도 역시 계산할 수 없습니다. (5-3) 항 때문인데요. 여기에 약간의 트릭을 써볼 수 있습니다. (5-3) 항은 KL Divergence 이기 때문에 반드시 0보다 크거나 같은 값을 갖습니다. 따라서 (5-3) 항을 떼어놓고 생각했을 때 반드시 $\log_\theta p(x)$는 다음을 만족합니다.

\[\log_\theta p(x) \ge \mathbb{E}_z \left[ \log p_\theta(x \mid z) \right] - D_\text{KL} \left( q_\phi(z \mid x) \ \| \ p_\theta(z) \right) = \mathcal{L}(x, \theta, \phi) \notag\]

항상 학습 데이터의 우도는 부등식의 우변보다 크거나 같습니다. 베이지안 추론에서 $p(x)$를 evidence 라고 하는데, 이 evidence의 최솟값이 부등식의 우변이 되어 이를 Evidence Lower Bound (ELBO)라고 부릅니다. 여기서부터 VAE를 학습하기 위한 손실 함수(loss function)은 ELBO인 $\mathcal{L}(x, \theta, \phi)$ 가 됩니다. 이제 우리는 학습 데이터의 우도를 최대화하는 것을 ELBO를 최대화하는 것으로 바꾸어 생각할 수 있습니다.

\[\theta^\ast, \phi^\ast = \arg\max_{\theta, \phi} \sum^N_{i=1} \mathcal{L}\left( x^{(i)}, \theta, \phi \right). \notag\]

참고로 디코더의 Likelihood 기댓값 (5-1)이 커져야 하고 인코더와 사전 분포인 가우시안 분포 사이의 차이 (5-2)가 줄어들어야 ELBO가 최대화된다는 것도 논리적으로 이해할 수 있게 됩니다. 조금 더 풀어서 설명하자면 (5-1) 항은 입력 데이터를 재구현하는 것과 관련이 있고, (5-2) 항은 사후 분포가 사전 분포로 근사하는 것과 관련이 있습니다.

Reparametrization Trick

VAE를 학습하는 방법은 손실 함수에 대한 정의까지 마무리 되었습니다. 그런데 여기서 (5-1) 항을 잘 살펴보면 다음과 같은 샘플링 과정이 포함되어 있습니다.

\[z \sim q_\phi(z \mid x) \notag\]

따라서 이 과정은 stochastic하다고 할 수 있습니다. 이런 과정은 순전파에선 문제가 되지 않습니다. Feed-forward 계산은 단순히 $q_\phi(z \mid x)$ 에서 $z$를 여러개 샘플링하여 $p_\theta(x \mid z)$를 계산하면 되기 때문입니다. 문제는 역전파 과정에서 발생합니다. 당연히 우리는 gradient descent/ascent를 이용하여 학습을 할텐데 샘플링은 미분이 가능한 연산이 아니기 때문에 gradient descent/ascent를 사용하기 어려워집니다. 기울기를 계산하기 위해서는 확률 변수인 $z$가 deterministic 해야 하기 때문이죠.

:bulb: 엄밀하게는 값을 구할 수 있으나 그 추정값의 분산이 너무 커서 의미가 없다고 합니다. 자세한 내용은 이 곳을 참고하시기 바랍니다.

Figure 2. Reparametrization Trick.

그래서 VAE에서는 이 문제를 해결하기 위해 reparametrization trick을 사용합니다. 어떤 방법을 이용해 위에서 말한 대로 $z$를 deterministic하게 만들어 주는거죠. 원래대로라면 위 이미지의 왼쪽처럼 $z$는 다음과 같이 샘플링이 됩니다.

\[z \mid x \sim \mathcal{N}(\mu_{z \mid x}, \Sigma_{z \mid x}) \notag\]

하는 일은 간단하게 평균과 표준편차를 이용해 샘플링을 하는거죠. 이 과정을 $\epsilon \sim \mathcal{N}(0, I)$를 이용해서 다음과 같이 reparametrization할 수 있습니다.

\[z = g_\phi (\epsilon, x) = \mu_\phi(x) + \epsilon \odot \Sigma_\phi (x) \notag\]

재밌게도 $z$는 기존 샘플링한 값과 크게 달라지지 않습니다. 표준 편차를 적당한 노이즈를 곱해 평균에 더하기 때문에 기존 가우시안 분포에서 샘플링하는 것과 비슷한 값이 나오기 때문이죠. 하지만 이렇게 reparametrize를 하면 역전파 시에도 $z$에 대해 미분을 할 수 있게 되고 $(\mu, \Sigma)$에 대해서 미분이 가능해집니다. Reparametrization trick을 사용한 VAE의 최종적인 구조는 아래와 같습니다.

Figure 3. Reparametrized Variational Autoencoder.

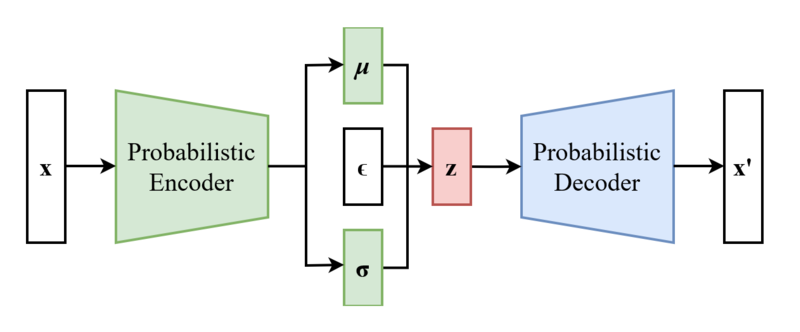
Loss Function for Gaussian Case

마지막으로 손실 함수를 실제로 구현할 때 어떻게 해야하는지 알아보도록 하겠습니다. 우선 손실 함수인 ELBO를 다시 보도록 하겠습니다.

\[\mathcal{L}(x, \theta, \phi) = \mathbb{E}_z \left[ \log p_\theta(x \mid z) \right] - D_\text{KL} \left( q_\phi(z \mid x) \ \| \ p_\theta(z) \right) \notag\]

첫 번째 항은 계속 언급하였듯이 디코더의 reconstruction error 입니다. 따라서 일반적인 binary cross-entropy로 계산하면 됩니다. 실제 구현할 때 마지막 디코더의 아웃풋 형태에 따라 다음과 같이 쓸 수 있겠죠.

# Binary cross entrop
BCE = torch.nn.BCELoss(recon_x, x)

# MultVAE와 같이 Multinomial distribution인 경우
BCE = -torch.mean(torch.sum(F.log_softmax(recon_x, 1)*x, -1))

두 번째 항이 조금 복잡한데요. $q_\phi(z \mid x)$와 $p_\theta(z)$ 모두 가우시안 분포를 가정하고 있기 때문에 해석적(analytic)인 결과를 얻을 수 있습니다.

\[q_\phi(z \mid x) \sim \mathcal{N}(z; \mu, \sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} \exp \left( -\frac{(z-\mu)^2}{2\sigma^2} \right), \qquad p_\theta(z) \sim \mathcal{N}(z; 0, \mathbb{I}) = \frac{1}{\sqrt{2\pi}} \exp\left( -\frac{z^2}{2} \right)\]

Kullback-Leibler divergence의 정의에 따라 두 번째 항을 다음과 같이 풀어서 쓸 수 있습니다.

\[\begin{align*} D_\text{KL} \left( q_\phi(z \mid x) \ \| \ p_\theta(z) \right) &= \int q_\phi(z \mid x) \cdot \log \left( \frac{p_\theta(z)}{q_\phi(z \mid x)} \right) \ dz \\ &= \int q_\phi(z \mid x) \cdot \log \left( \frac{\frac{1}{\sqrt{2\pi}} \exp\left( -\frac{z^2}{2} \right)}{\frac{1}{\sigma \sqrt{2\pi}} \exp \left( -\frac{(z-\mu)^2}{2\sigma^2} \right)} \right) \ dz \\ &= \int q_\phi (z \mid x) \cdot \log \left( \sigma \cdot \exp \left( -\frac{z^2}{2} + \frac{(z-\mu)^2}{2\sigma^2} \right) \right) \; dz \\ &= \int q_\phi(z \mid x) \cdot \left( \log \sigma -\frac{z^2}{2} + \frac{(z-\mu)^2}{2\sigma^2} \right) \; dz \tag{*} \end{align*}\]

여기서 마지막 $(*)$은 $q_\phi(z \mid x)$에 대한 기댓값으로 다시 쓸 수 있습니다.

\[\begin{align*} (*) &= \mathbb{E}_{q_\phi(z \mid x)} \left( \log \sigma -\frac{z^2}{2} + \frac{(z-\mu)^2}{2\sigma^2} \right) \\ &= \log \sigma - \frac{1}{2} \mathbb{E}_q \left[ z^2 \right] + \mathbb{E}_q \left[ \frac{(z-\mu)^2}{2\sigma^2} \right] \tag{**} \end{align*}\]

분산은 확률변수와 기댓값 사이의 차이를 제곱한 것의 기댓값이므로 식 $(**)$의 마지막 항은 $\mathbb{E}_q \left[ \frac{(z-\mu)^2}{2\sigma^2} \right] = \frac{\sigma^2}{2\sigma^2} = \frac{1}{2}$ 가 됩니다. 따라서 위 식을 다시 쓰면 다음과 같습니다.

\[(**) = \log \sigma - \frac{1}{2} \underbrace{\mathbb{E}_q \left[ z^2 \right]}_{(***)} + \frac{1}{2} \notag\]

마지막으로 $(***)$를 정리하면 손실 함수의 두 번째 항을 정리할 수 있습니다. $z$를 $z - \mu + \mu$ 로 치환하여 계산을 다시 해보겠습니다.

\[\begin{align*} (***) &= \mathbb{E}_q \left[ (z - \mu + \mu)^2 \right] \\ &= \mathbb{E}_q \left[ (z-\mu)^2 + 2\mu(z-\mu) + \mu^2 \right] \\ &= \mathbb{E}_q \left[ (z-\mu)^2 \right] + 2 \mu \cdot \mathbb{E}_q \left[ (z-\mu) \right] + \mu^2 \\ &= \sigma^2 + \mu^2 \end{align*}\]

따라서 손실 함수의 두 번째 항은 다음과 같이 정리할 수 있습니다.

\[D_\text{KL} \left( q_\phi(z \mid x) \ \| \ p_\theta(z) \right) = -\frac{1}{2} \left( 1 + \log \sigma^2 - \sigma^2 - \mu^2 \right).\]

PyTorch 기준, 두 번째 항에 대한 코드는 다음과 같습니다.

KLD = -0.5 * torch.mean(torch.sum(1 + logvar - mu.pow(2) - logvar.exp(), dim=1))

References

[1] CS231n Lectures 12 by Fei-Fei Li & Justin Johnson & Serena Yeung