Variational Autoencoders for Collaborative Filtering

Posted Aug 6, 2022 Updated Jun 9, 2023

By Jay Han

views 12 min read

Liang, Dawen, et al. “Variational autoencoders for collaborative filtering.” Proceedings of the 2018 world wide web conference. 2018.

Introduction

Latent factor 모델은 단순함과 효율성을 바탕으로 협업 필터링 문제에 여전히 많이 사용되고 있습니다. 하지만 이런 모델들은 본질적으로 선형적이기 때문에 modeling capacity 측면에서 한계를 보입니다. 저자는 이런 문제를 보완하기 위해 implicit feedback에 대한 협업 필터링 모델에 Variational Autoencoder (VAE)를 도입하였습니다. VAE는 선형적인 latent factor 모델을 일반화할 수 있고, 더 나아가 비선형 확률적 잠재 변수 모델로 확장할 수 있기 때문입니다. 또한 Multinomial likelihood를 이용하여 implicit feedback을 모델링하였고, 기존에 많이 사용되는 likelihood인 Gaussian이나 로지스틱 함수보다 추천에 더 적합하다는 사실을 확인했다고 합니다.

또한 사용자의 희소한 데이터를 활용하고 오버피팅을 피하기 위해 확률적인 잠재 변수 모델을 구축하였으며, 경험적으로 데이터의 부족함과 상관 없이 베이지안 접근법을 통해 강건한 모델을 구축할 수 있는 것을 확인하였다고 합니다.

Method

본 논문에선 다음의 Notation을 사용합니다.
- Users : $u \in {1, \cdots, U}$
- Items : $i \in { 1, \cdots, I }$
- Click matrix $\mathbf{X} \in \mathbb{N}^{U \times I}$
- $\mathbf{x}_u = [ x_{u1}, \cdots, x_{uI} ]^\top \in \mathbf{N}^I$

Model

우선 사용자 $u$마다 Gaussian prior로부터 $K$ 차원의 latent representation $z_u$를 샘플링합니다. $z_u$는 비선형 함수 $f_\theta(\cdot) \in \mathbb{R}^I$를 거쳐서 히스토리 $x_u$로부터 $I$ 개의 아이템에 대한 확률 분포 $\pi(z_u)$를 생성하게 됩니다. $N_u = \sum_i x_{ui}$에 대해서 다음처럼 쓸 수 있습니다.

\[\mathbf{z}_u \sim \mathcal{N}(0, \mathbf{I}_K), \quad \pi(\mathbf{z}_u) \propto \exp \{ f_\theta (\mathbf{z}_u) \}, \quad \mathbf{x}_u \sim \text{Mult}(N_u, \pi(\mathbf{z}_u))\]

여기서 $f_\theta(\cdot)$은 MLP가 됩니다. 만약 $f_\theta(\cdot)$이 선형 함수거나 Gaussian likelihood인 경우 전통적인 Matrix Factorzation과 같아집니다.

위 설정에서 사용자 $u$에 대한 log-likelihood는 다음과 같습니다.

\[\log p_\theta (\mathbf{x}_u \mid \mathbf{z}_u) \overset{c}{=} \sum_i x_{ui} \log \pi_i(\mathbf{z}_u).\]

여기까지 보면 알 수 있듯 저자들은 Click matrix를 모델링할 때 Multinomial distribution이 적절하다고 판단하였습니다. 각 사용자에 대해 Click matrix의 likelihood가 non-zero entry인 경우에 대해 확률값을 부여하는데, 이때 사용자마다의 확률값은 그 합이 1이 되기 때문에 저자들은 Click matrix를 재구현하는 것보다는 top-N ranking loss 아래에서 잘 작동할 것이라고 예상합니다.

Variational Inference

이제 $f_\theta(\cdot)$의 파라미터인 $\theta$를 추정해야 합니다. 이를 위해선 Posterior인 $p(\mathbf{z}_u \mid \mathbf{x}_u)$를 계산해야 하지만 intractable하다는 문제가 있습니다. 따라서 Variational inference를 이용해 근사 분포인 $q(\mathbf{z}_u)$를 대신 계산해야 합니다. Variational inference의 목적은 두 분포의 차이인 $\text{KL}(q(\mathbf{z}_u) \; | \; p(\mathbf{z}_u \mid \mathbf{x}_u) )$를 최소화하여 Free parameter ${ \boldsymbol{\mu}_u, \boldsymbol{\sigma}_u^2 }$를 최적화하는 것입니다.

\[q(\mathbf{z}_u) \sim p(\mathbf{z}_u \mid \mathbf{x}_u), \quad q(\mathbf{z_u}) = \mathcal{N}(\boldsymbol{\mu}_u, \text{diag}\{\boldsymbol{\sigma}^2_u \}).\]

Amortized inference and the variational autoencoder

Variational inference에서 사용자와 아이템의 수가 많아지기 시작하면 최적화해야 하는 파라미터의 수 역시 점점 증가하게 되고, 이는 실제 추천 시스템에서 큰 bottleneck이 될 수 있습니다. 이를 해결하기 위해 variational parameter를 일반적으로 추론 모델 (inference model)이라고 부르는 데이터에 의존적인 함수로 치환하였습니다.

\[g_\phi (\mathbf{x}_u) \equiv \left[ \mu_\phi(\mathbf{x}_u), \sigma_\phi(\mathbf{x}_u) \right] \in \mathbb{R}^{2K}.\]

그러면 기존의 $q(\mathbf{z}_u)$는 다음과 같이 쓸 수 있습니다.

\[q_\phi(\mathbf{z_u} \mid \mathbf{x}_u) = \mathcal{N} \left( \mu_\phi(\mathbf{x}_u), \text{diag} \left\{ \sigma_\phi^2 (\mathbf{x}_u) \right\} \right)\]

따라서 입력 데이터 $\mathbf{x}_u$ 를 이용해 intractable한 posterior $p(\mathbf{z}_u \mid \mathbf{x}_u)$ 를 $q_\phi(\mathbf{z}_u \mid \mathbf{x}_u)$ 로 근사시키게 됩니다.

모델을 학습할 때는 ELBO를 최대화하는 방향으로 학습합니다.

\[\begin{aligned} \log p(\mathbf{x}_u ; \theta) &\geq \mathbb{E}_{q_\phi (\mathbf{z}_u \mid \mathbf{x}_u)} \left[ \log p_\theta (\mathbf{x}_u \mid \mathbf{z}_u)\right] - \text{KL}(q_\phi(\mathbf{z}_u \mid \mathbf{x}_u) \| p(\mathbf{z}_u)) \\ &\equiv \mathcal{L}(\mathbf{x}_u; \theta, \phi) \end{aligned}\]

여기서 ${\mathbf{z}_u} \sim q_\phi $ 샘플링을 통해 ELBO에 대한 불편향 추정을 하고 SGA(Stochastic Gradient Ascent)를 통해 최적화하는데요. 이때 $\phi$ 에 대해서 그라디언트를 계산하는 것이 불가능합니다. 따라서 $\mathbf{z}_u$ 를 $\mathbf{x}_u$ 로 reparametrize하여 $\phi$ 에 대해 그라디언트를 계산해 역전파하게 됩니다.

\[\boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I}_K) \qquad \mathbf{z}_u = \mu_\phi (\mathbf{x}_u) + \boldsymbol{\epsilon} \odot \sigma_\phi (\mathbf{x}_u).\]

Alternative interpretation of ELBO

ELBO를 다시 한 번 살펴보겠습니다.

\[ELBO = \mathbb{E}_{q_\phi (\mathbf{z}_u \mid \mathbf{x}_u)} \left[ \log p_\theta (\mathbf{x}_u \mid \mathbf{z}_u)\right] - \text{KL}(q_\phi(\mathbf{z}_u \mid \mathbf{x}_u) \| p(\mathbf{z}_u))\]

여기서 첫 번째 항은 Reconstruct Error, 두 번째 항은 Regularization으로 볼 수 있습니다. 논문에서 제안하는 추천 알고리즘의 기반이 되는 VAE는 강력한 생성 모델이기 때문에 기존 데이터를 너무 잘 샘플링하는 경우가 있습니다. 물론 생성 모델이 잘 샘플링하면 좋지만 추천을 위해서는 재구현 성능을 조금 희생해서 추천 성능을 높여야 합니다. 이런 관점에서 저자들은 두 번째 항에 Regularization을 조절하는 파라미터인 $\beta$ 를 넣어서 다음과 같은 손실 함수를 사용하였습니다.

\[\mathcal{L}(\mathbf{x}_u; \theta, \phi) = \mathbb{E}_{q_\phi (\mathbf{z}_u \mid \mathbf{x}_u)} \left[ \log p_\theta (\mathbf{x}_u \mid \mathbf{z}_u) \right] - \color{red}{\beta} \color{black} \cdot \text{KL}(q_\phi(\mathbf{z}_u \mid \mathbf{x}_u) \| p(\mathbf{z}_u))\]

만약 $\beta$ 를 1보다 작게 설정하면 Prior constraint $\frac{1}{U} \sum_u q(\mathbf{z} \mid \mathbf{x}_u) \approx p(\mathbf{z}) = \mathcal{N}(\mathbf{z}; 0, \mathbf{I}_K)$ 의 영향을 줄일 수 있습니다. 그러면 과거 사용자 이력으로부터 새로운 사용자의 데이터를 잘 생성하진 못하게 되지만 이를 통해 성능 향상에 기여하는 것을 확인할 수 있었다고 합니다.

그러면 이제 적절한 $\beta$ 를 선택하는 방법을 생각해봐야 하는데요. 저자들은 KL Annealing을 사용했다고 합니다. 우선 $\beta = 0$ 부터 학습을 시작해서 매 epoch마다 $\beta = 1$ 까지 값을 점진적으로 증가시키는데요. 이때 매 epoch마다 $\beta$ 를 조금씩 증가시키기 때문에 추가적인 학습이 필요가 없습니다. $\beta=0$ 부터 시작하기 때문에 처음에는 재구현 성능에 초점을 맞추다가 epoch이 증가할 수록 Regularization을 수행하는 형태입니다. 실제 구현 시에는 total_anneal_steps와 anneal_cap을 둬서 일종의 Learning rate와 Maximum annealing constant 역할을 하게 만듭니다.

  
if self.total_anneal_steps > 0:
    self.anneal = min(self.anneal_cap, 1. * self.update_count / self.total_anneal_steps)
else:
    self.anneal = self.anneal_cap

KL Annealing을 사용했을 때 성능이 비약적으로 올라가는 것을 확인할 수 있었다고 합니다.

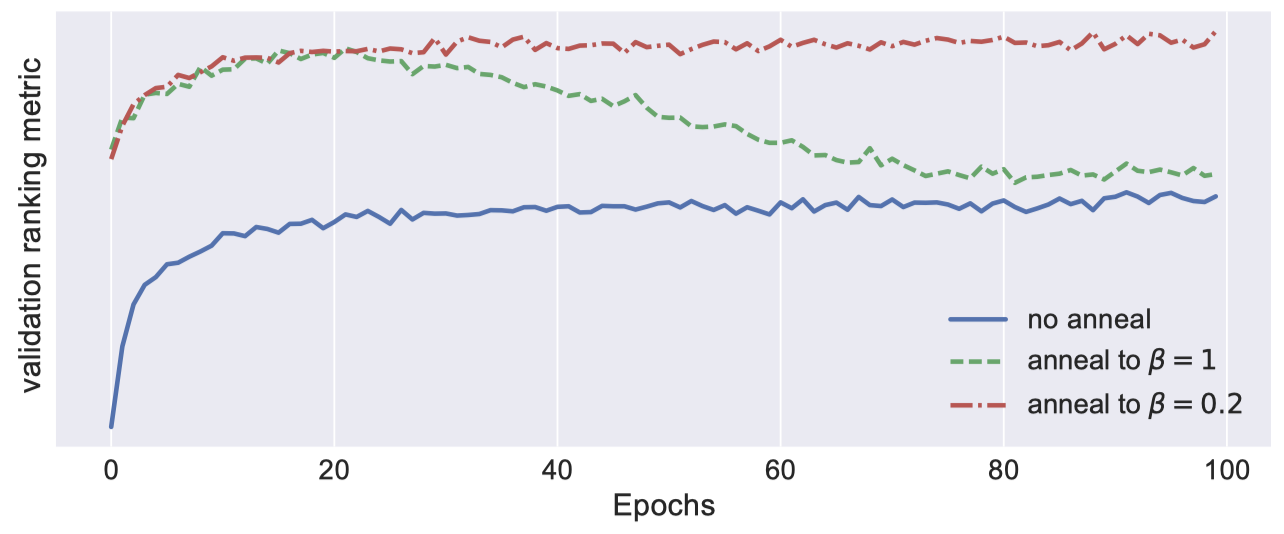
위 그림은 KL Annealing을 사용했을 때의 성능을 비교한 것입니다. 빨간 점선은 anneal_cap = 0.2로 설정하여 최대 $\beta$ 가 0.2가 한 결과입니다. 초록색 점선은 $\beta$ 를 1까지 증가시킨 결과인데, 여기서 이미 $\beta = 0.2$ 근처에서 최적의 성능을 보이는 것을 알 수 있습니다. 저자들은 KL Annealing과 Multinomial likelihood를 사용한 부분적으로 regularized된 VAE 기반 CF 모델을 Mult-VAE로 부릅니다.

Computational Burden

이 논문 이전의 Autoencoder 기반 모델들은 대부분 (사용자, 아이템) 순서쌍을 하나의 데이터 단위로 설정하지만 Mult-VAE는 사용자 한 명을 단위로 합니다. 다시 말해서 Click matrix에서 각 엔트리가 아닌 각 행을 단위로 하게 되죠. 이렇게 하면 네거티브 샘플링이 필요가 없어져서 계산이 용이해집니다. 대신 Multinomial probability를 계산할 때 computationally expensive할 수 있지만 실험 결과 50K 미만이면 큰 문제가 없다고 합니다.

Prediction

이력 데이터 $\mathbf{x}$ 가 주어지면 un-normalized predicted multinomial probability $f_\theta(\mathbf{z})$ 를 계산해 순위를 매깁니다. 이때 $\mathbf{x}$ 에 대한 latent representation $\mathbf{z}$ 는 $\mathbf{z} = \mu_\phi(\mathbf{x})$ 가 됩니다.

VAEs on Sparse Data

VAE는 크고 희소한 고차원의 데이터에 대해 잘 학습되지 않는, 즉 underfitting한다는 연구 결과가 있는데요. 실제로 annealing을 하지 않거나 $\beta=1$로 KL Annealing을 하게 되면 그런 모습을 볼 수 있었다고 합니다. 하지만 위에서 언급했듯이 $\beta < 1$로 설정하여 학습이 잘 되도록하여 성능 문제를 해결했습니다. 진정한 의미에서의 생성 모델은 아니겠지만 협업 필터링 관점에서는 사용자의 이력에 기반한 올바른 추천을 해주게 됩니다.

This post is licensed under CC BY 4.0 by the author.