Neural Collaborative Filtering vs. Matrix Factorization
Rendle, Steffen, et al. “Neural collaborative filtering vs. matrix factorization revisited.” Fourteenth ACM conference on recommender systems. 2020.
최근 NCF를 구현해서 사용하면서 이 알고리즘이 ALS 같은 Matrix Factorization 계열 알고리즘보다 어떤 점에서 더 좋은지 궁금했습니다. Tabular data를 학습하여 예측하는 다소 클래식한 문제에 대해서는 뉴럴 네트워크 계열의 알고리즘이 크게 재미를 못보는 경우가 많은데 NCF는 논문이 발표되었던 당시에 SOTA 라는 것이 조금 의아했죠. 물론 단순한 Tabular data에 대한 학습은 아니었기에 그럴 수 있다는 생각은 했습니다.
이 논문은 이런 부분을 매우 자세히 파헤칩니다. NCF와 Matrix Factorization의 성능을 다시 비교하고 이론적인 인사이트를 제시합니다. 이 논문의 결론은 이렇습니다.
:bulb: MLP 기반의 유사도를 모델링하는 방법은 여러 측면에서 Dot Product와 같은 Matrix Factorization 보다 낫지 않음.
Introduction
임베딩 기반의 모델은 최근 몇 년간 협업 필터링 (Collaborative Filtering)에서 많은 성공을 거두었습니다. 이런 모델들의 핵심은 두 개 이상의 임베딩을 결합하는 것입니다. 예를 들어 사용자 정보 임베딩과 아이템 정보 임베딩을 결합하여 사용자의 선호도를 나타내는 단일 스코어를 얻어내는 것이죠. 이는 임베딩 공간에서 일종의 유사도 함수로 생각할 수 있습니다.
전통적으로 유사도에 대해서는 Dot product나 등이 쓰였었는데 최근에는 Neural network를 이용해 유사도 함수를 학습하는 경우가 많아졌습니다. 그 중에서 가장 유명한 것이 Neural Collaborative Filtering인데요. 이런 방법들의 논리적 근거는 MLP가 “general function approximators”로서 Dot product와 같은 고정적인 유사도 함수보다 더 나을 것이란 생각입니다.
저자들은 NCF와 Dot product를 비교를 했습니다. NCF 논문에서의 실험들을 다시 수행하였고, 그 결과 잘 구성한 Dot product가 MLP보다 더 낫다는 것을 알게 되었다고 이야기 합니다. MLP가 물론 universal function approximator이지만 Dot product만큼 성능이 나오지 않는데다 추후 추론 속도까지 생각해보면 Dot product가 더 낫다고 합니다. 궁극적으로는 여러 임베딩을 결합하여 MLP 기반 유사도 함수를 모델링할 때는 매우 주의를 기울여서 사용해야 한다고 말합니다.
Definitions

Dot Product
두 임베딩을 결합하는 가장 일반적인 방법은 Dot product 입니다.
\[\phi^\text{dot} ( \mathbf{p} + \mathbf{q}) := \langle \mathbf{p}, \mathbf{q} \rangle = \mathbf{p}^T \mathbf{q} = \sum^d_{f=1} p_f q_f. \label{eq1} \tag{1}\]$\mathbf{p}$와 $\mathbf{q}$가 free model parameter이면 위 식은 Matrix Factorization과 동일해집니다.
Dot product에 편향을 추가하는건 일반적인 방법으로 다음과 같습니다.
\[\phi^{\text{dot}} (\mathbf{p}, \mathbf{q}) := b + p_1 + q_1 + \langle \mathbf{p}_{[2, \cdots, d]}, \mathbf{q}_{[2, \cdots, d]} \rangle. \label{eq2} \tag{2}\]Learned Similarity
MLP에서 하나의 레이어는 함수 $f : \mathbb{R}^{d_\text{in}} \to \mathbb{R}^{d_\text{out}}$으로 정의할 수 있습니다. $W \in \mathbb{R}^\text{in $\times$ out}$, $\mathbf{b} \in \mathbb{R}^\text{out}$, 활성화 함수 $\sigma : \mathbb{R} \to \mathbb{R}$에 대해서 다음과 같습니다.
\[\mathbf{f}_{W, \mathbf{b}}(\mathbf{x}) = \boldsymbol{\sigma}(W \mathbf{x} + \mathbf{b}), \quad \boldsymbol{\sigma}(\mathbf{z}) = [\sigma(z_1), \cdots, \sigma(z_\text{out})]. \label{eq3} \tag{3}\]NCF 논문에서는 Dot product를 학습 가능한 유사도 함수로 대체하는 방법을 제안합니다. 사용자 정보 임베딩과 아이템 정보 임베딩을 concatenate하여 MLP를 적용합니다.
\[\phi^\text{MLP} (\mathbf{p}, \mathbf{q}) := \mathbf{f}_{W_l, \mathbf{b}_l} (\cdots \mathbf{f}_{W_1, \mathbf{b}_1} ([\mathbf{p}, \mathbf{q}]) \cdots). \label{eq4} \tag{4}\]여기에 Neural network 기반의 Generalized Matrix Factorization (GMF)을 결합하여 Neural Matrix Factorization (NeuMF)라는 모델을 제안하였습니다.
\[\phi^\text{GMF}(\mathbf{p}, \mathbf{q}) := \sigma(\mathbf{w}^T (\mathbf{p} \ \odot \ \mathbf{q})) = \sigma(\langle \mathbf{w} \ \odot \ \mathbf{p}, \mathbf{q} \rangle) = \sigma \left( \sum^d_{f=1} w_f p_f q_f \right). \label{eq5} \tag{5}\] \[\phi^\text{NeuMF} (\mathbf{p}, \mathbf{q}) := \phi^\text{MLP}(\mathbf{p}_{[1, \cdots, j]} , \mathbf{q}_{[1, \cdots, j]}) + \phi^\text{GMF}(\mathbf{p}_{[j+1, \cdots, d]} , \mathbf{q}_{[j+1, \cdots, d]}) \label{eq6} \tag{6}\]Revisiting NCF Experiments
논문에서는 총 네 개의 모델을 비교했습니다.
- Dot Product (MF)
- L2 regularization을 사용한 logistic loss를 SGD로 최소화하는 방식으로 학습하였습니다.
- Negative sampling을 사용했습니다.
- Learned Similarity (MLP)
- MLP + GMF (NeuMF)
- MLP + GMF pretrained (NeuMF)
- MLP와 GMF 각각을 학습한 후 Fine-tuning하는 방식으로 기존 NCF 논문에서 가장 성능이 좋다고 언급한 바 있습니다.
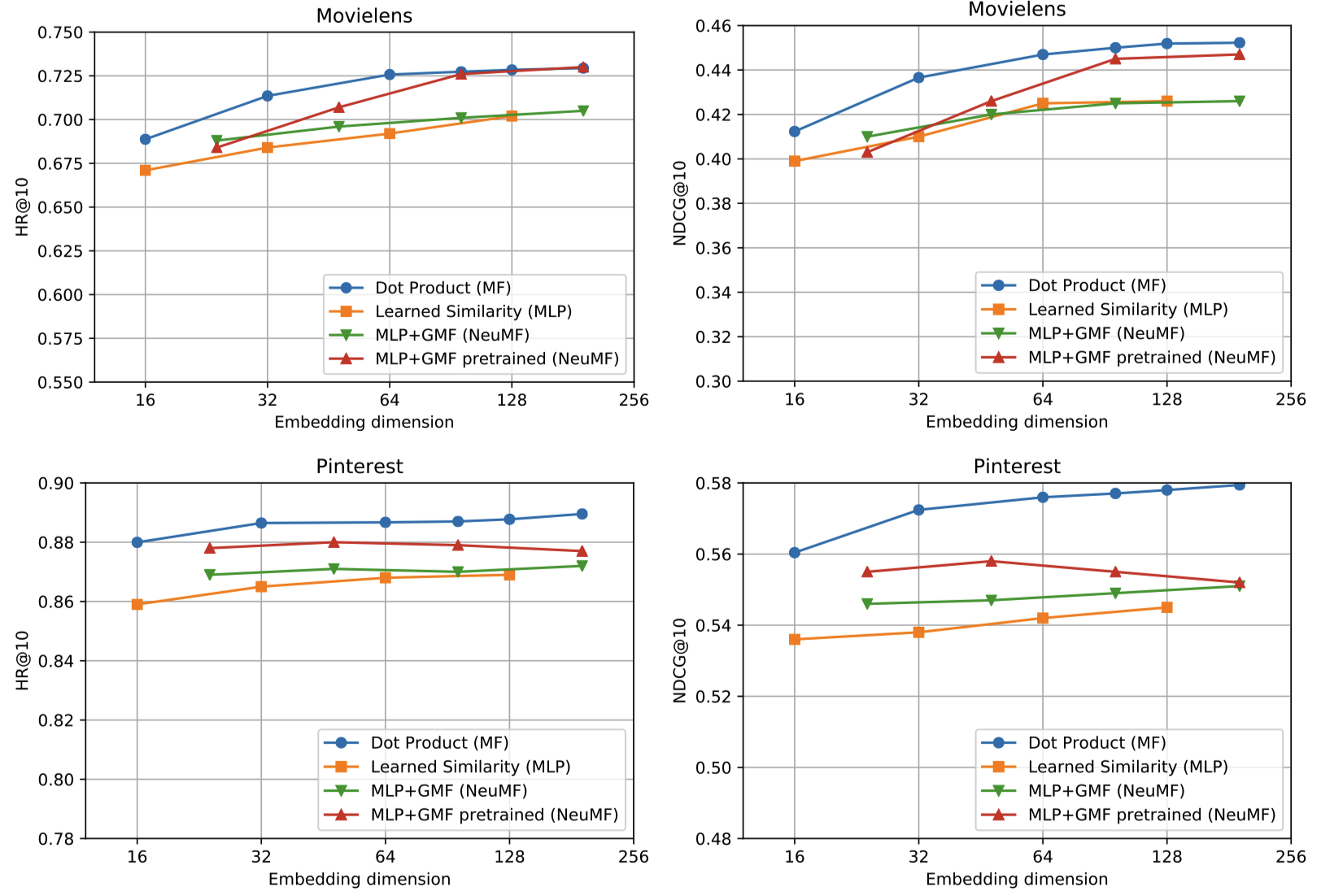
실험 결과는 “모든 데이터셋에서 MF의 성능이 가장 좋다.” 로 요약할 수 있습니다.
On the performance of GMF
하나 짚고 넘어가야 할 것은 GMF는 Dot product에 가중치를 부여한 것 외에는 MF와 차이가 없음에도 성능에서 제법 차이가 있다는 점입니다. 실제 학습도 같은 loss 함수와 negative sampling을 사용했습니다. 저자들은 GMF가 MF 보다 성능이 낮은 것에 대해서 다음과 같이 분석했습니다.
일반적으로 베이스라인 기법을 튜닝하고 적절하게 세팅하는 것이 어렵기 때문입니다.
$\phi^\text{GMF}$ 은 $\eqref{eq5}$ 에서 볼 수 있듯이 새로운 모델 파라미터인 $\mathbf{w}$를 사용합니다. 하지만 해당 파라미터는 regularization의 영향을 제대로 받지 못합니다.
Dot product 에 아무런 영향을 미치지 않지만 부정적인 영향을 끼칠 수 있습니다.
- \[L(P, Q, \mathbf{w}, \lambda) = \ell \left( \left\{ \phi_\mathbf{w}^\text{GMF} (\mathbf{p}, \mathbf{q}) : \mathbf{p} \in \text{Rows}(P), \; \mathbf{q} \in \text{Rows}(Q) \right\} \right) + \lambda \left( \| P \|^2_F + \|Q\|^2_F \right)\]
위 loss function에서 첫 항은 모델 아웃풋에 의존하고 두 번째 항은 regularization term입니다. 자세히 보면 $P$와 $Q$는 regularized지만 $\mathbf{w}$는 그렇지 않습니다.
만약 모델 파라미터들을 positive scalar $a$로 스케일링하면 모델 아웃풋은 바뀌지 않고 다음의 식이 성립합니다.
- \[L(P, Q, \mathbf{w}, \lambda) = L\left( \frac{1}{a}P, \frac{1}{a}Q, a^2 \mathbf{w}, a^2 \lambda \right).\]
- Change of variable을 이용해서 $a = \sqrt{\frac{\bar{\lambda}}{\lambda}}$로 두면 모델 아웃풋은 바뀌지 않습니다만 결국 regularizaiton에 영향을 받지 않게 됩니다. 여기서 만약 $\lambda = 0$ 이라면 학습이 이루어지지 않아 numerical instability를 야기합니다.
마지막으로 GMF는 단순한 Dot product와 비교하여 모델의 표현력을 높여주지 못합니다. 가중치 벡터인 $\mathbf{w}$가 단순히 임베딩 행렬인 $P$와 $Q$에 흡수되기 때문입니다.
Learning a Dot Product with MLP is Hard
MLP는 익히 universal function approximator로 알려져 있습니다. 이 때문에 MLP가 Dot product보다 더 나은 성능을 보여줄 것이란 기대를 하게 되지만 실제론 그렇지 않다는 것을 위에서 확인했습니다. 실제 MLP를 학습할 때는 더 많은 데이터가 필요하고 원하는 타겟 함수를 학습할 때 어려움을 마주하게 되기 때문인데요. 그래서 본 논문에서는 합성 데이터를 통해 MLP가 어느 정도로 Dot product에 근사하여 학습되는지 알아보았습니다. 실험에 대한 자세한 세팅은 논문을 참고하시길 바랍니다.

회색 선보다 높은 곳에 그래프가 위치하는 경우 매우 유의한 수준에서 MLP와 Dot product의 성능에 차이가 나는 것을 의미합니다. 실험 결과 충분한 학습 데이터가 주어진 상태에서 적당히 많은 히든 레이어로 네트워크를 구성하면 MLP가 Dot product에 근사한 결과를 얻을 수 있는 것을 확인했습니다. 이 실험을 통해 MLP를 학습하여 Dot product만큼의 성능을 내는 것이 쉽지 않다는 것을 알 수 있습니다. 게다가 실제 비슷한 성능을 얻었다고 하더라도 그 때 MLP는 매우 복잡한 모델이 되기 떄문에 여러 측면에서 Dot product보다 더 나은 점이 없게 됩니다.