Mean Average Precision 이해하기
들어가며
Ranking task를 공부하다 보면 가장 많이 보게 되는 메트릭 중 하나가 바로 Mean Average Precision (MAP) 입니다. 처음 이 메트릭을 봤을 때는 이름 때문에 ‘Precision의 Average의 Mean이 뭐지?’ 하면서 헷갈렸던 기억이 있습니다. 실제로 추천 관련 업무를 하다 보면 ML 업무를 하시는 분들도 볼 때마다 헷갈리고, 이걸 비즈니스 현업 분들에게 설명해 드리기도 참 어렵다는 것을 쉽게 느낍니다.
저도 처음에는 이 메트릭을 업무에 사용하면서 많은 실수를 했었습니다. 정말 제대로 오개념이 박혀있었고, 이 오개념을 빼내서 제대로 된 산식을 넣는 데까지 어쩌다 보니 오랜 시간이 걸렸었는데요. 제가 어쩌다가 오개념에 빠져있었는지, 그리고 제대로 된 MAP는 어떤 것인지 본 포스트에서 자세히 다뤄보도록 하겠습니다.
문제의 시작
항상 그렇듯 우리는 모르는 것을 찾을 때 Stack Overflow를 참고합니다. 제게 오개념을 선사했던 것도 바로 Stack Overflow입니다. MAP@K에 대해서 찾기 위해 Mean average precision for recommendations 로 검색을 했죠. 그렇게 보게 된 질문글이 바로 이 글입니다.
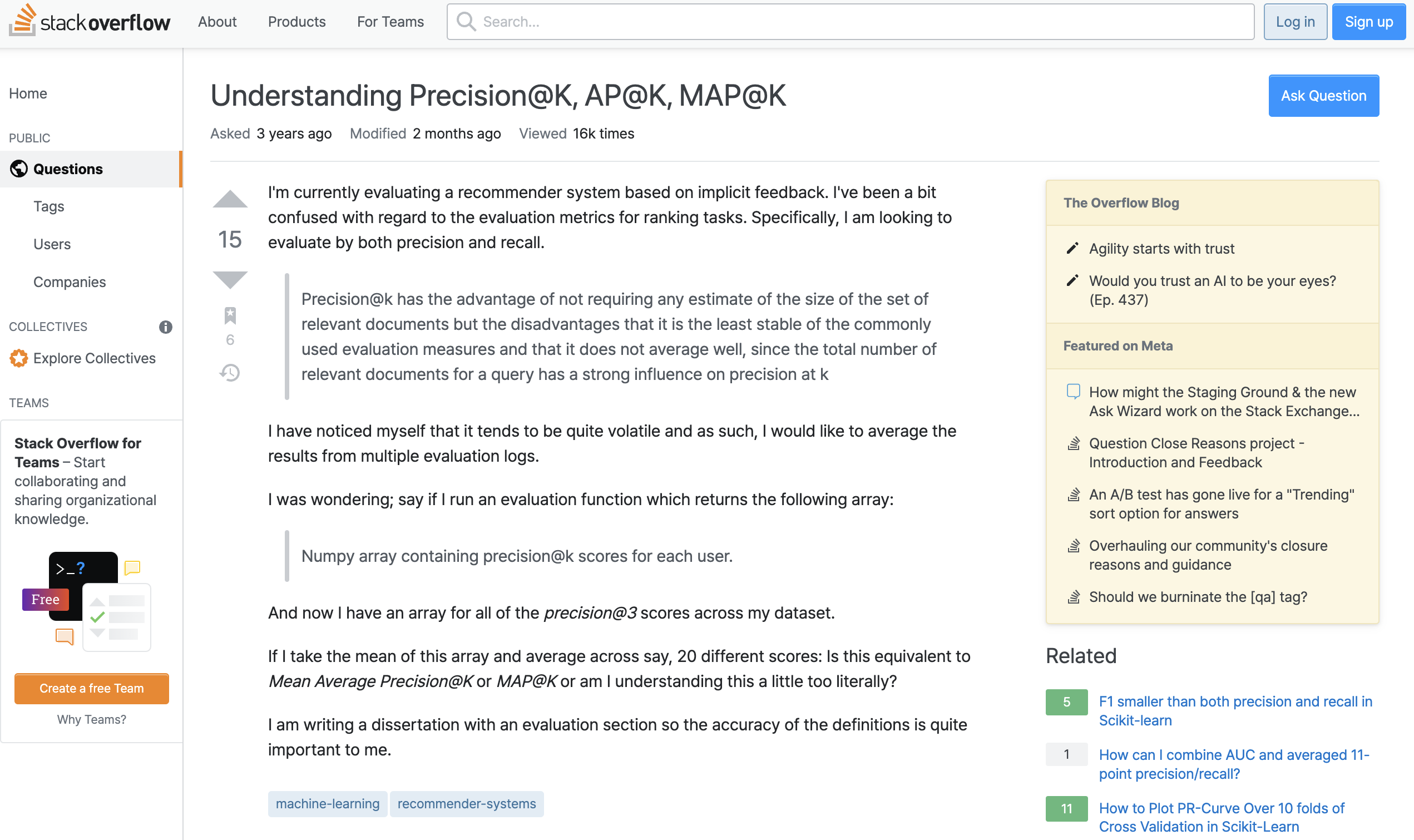
사실 질문 자체는 평범했습니다. $P@K$, $AP@K$, $MAP@K$ 를 졸업 논문에 써야 하는데 그 방법에 대한 질문이었죠. 문제는 이 질문에 대한 답변이었습니다. 답변의 내용 중 $AP@K$에 대한 설명은 다음과 같습니다.
❓ AP@K
The mean of $P@i$ for $i = 1, \cdots, K$.
$P@i$ 들의 평균이 $AP@K$ 라고 설명하고 있습니다. 잘 모르는 상태에서 보면 큰 의심을 하지 않을 겁니다. Average 니까 $P@K$들의 평균 아닐까? 라고 생각할 테니까요. 하지만 실제로 $AP@K$는 이렇게 계산하지 않습니다. 해당 답변의 댓글에도 설명이 잘못되어 있다는 지적이 매우 많습니다.
Average Precision
실제 $AP@K$는 다음과 같습니다.
\[AP@K = \frac{1}{m} \sum^K_{k=1} P(k) \cdot rel(k)\]$rel(k)$ 는 $k$ 번째 아이템이 올바른 추천이라면 $rel(k) = 1$, 아닌 경우 $rel(k) = 0$ 이 되는 함수입니다. 그리고 가장 중요하고 혼동을 유발하는 $m$은 실제 연관 있는 아이템의 수입니다. 즉 실제 연관 있는 아이템이 등장하였을 때의 $P@K$를 계산하고 이 값들의 평균인 거죠. 예를 들어 두 번째 아이템이 연관 없는 아이템이라면 $P@2$는 $AP@K$를 계산할 때 포함하지 않는 것이죠.
사실 이런 내용은 제 블로그에 있는 Learning to Rank 포스트에서도 한 번 다룬 적이 있는데, 깊은 이해를 위해 해당 포스트에서 다룬 예제를 다시 가져오겠습니다.

위 정의대로 계산한 $AP@10$은 다음과 같습니다.
- 첫 번째 쿼리에 대한 $AP(q)@10$은 $AP(q_1) = (1.0 + 0.67 + 0.5 + 0.44 + 0.5) / 5 = 0.62$
- 이 경우에는 연관이 있는 아이템이 다섯 개이므로 $m = 5$ 입니다.
- 두 번째 쿼리에 대한 $AP(q)@10$은 $AP(q_2) = (0.5 + 0.4 + 0.43) / 3 = 0.44$
- 이 경우에는 $m = 3$ 이겠죠.
이렇게 계산하는 이유는 여러 가지가 있겠지만 가장 큰 이유는 어떤 사용자의 실제 연관 있는 아이템 개수가 원래부터 적은 경우 불이익을 받는 경우가 발생할 수 있기 때문입니다. 예를 들어 연관 있는 아이템이 다섯 개인 사용자 $A$와 연관 있는 아이템이 한 개인 사용자 $B$가 있다고 가정해봅시다. 이때 연관 있는 아이템은 실제 추천과는 아무런 관계가 없다고 가정합니다. 이 경우에 Stack Overflow 답변에서 제시한 잘못된 방법으로 $AP@10$을 계산하면 어떻게 될까요? 아마 $B$에 대한 $AP@10$은 높은 확률로 $A$보다 낮을 겁니다. $B$가 추천 리스트 내에서 연관 있는 아이템이 등장할 확률이 $A$에 비해서 훨씬 낮기 때문이죠. 애초에 연관 있는 아이템의 수가 적으니까요. 이처럼 잘못된 방법으로 계산하게 되면 실제 추천 리스트의 품질과 상관없이 사용자의 연관 있는 아이템이 몇 개인지에 따라 메트릭 값이 결정됩니다.
그래서 올바른 메트릭 산식에서 $m$은 일종의 Normalizing 역할을 합니다. 제대로 계산한다고 했을 때 $A$의 경우 $m = 5$, $B$의 경우 $m = 1$ 이 될 겁니다. 그러면 $P(k) \cdot rel(k)$ 를 사용자별 연관 있는 아이템의 수로 나눠주기 때문에 만약에 연관 있는 아이템의 개수가 적더라도 페널티를 받지 않게 되죠. 따라서 추천 결과의 품질에 더 초점을 맞춰서 성능을 판단할 수 있게 됩니다.
조금 다른 형태의 Average Precision
하지만 이런 특이 케이스가 있을 수 있습니다. 추천 리스트에서 제공하는 아이템의 수는 10개인데 어떤 사용자는 지금까지 누적해 온 로그 데이터가 많아서 연관 있는 아이템의 개수가 20개인 거죠. 그러면 이 사용자의 경우 추천 리스트에서 제공하는 아이템이 모두 연관 있더라도 $m = 20$ 이기 때문에 반드시 손해를 보게 됩니다. $AP@10$의 최댓값이 무조건 0.5인 거죠.
이런 문제를 해결하기 위해서 위에서 정의한 Average Precision을 조금 변형한 버전을 사용하기도 합니다. 실제 Kaggle에서 사용하는 형태이고 최근에 가장 일반적으로 사용하는 형태입니다. [1]
\[AP@K = \frac{1}{\min(m, K)} \sum^K_{k=1} P(k) \cdot rel(k)\]이렇게 계산하는 $AP@K$를 Truncated Average Precision at $K$라고 부르기도 합니다. [2] 이 식을 이용하면 아까의 특이 케이스도 보정할 수 있게 됩니다. Normalizing constant 가 20이 아니라 10이 되니까요.
구현
$AP@K$를 Python으로 구현하는 것은 간단합니다. 실제 연관 있는 아이템이 없는 사용자에 대해서는 $AP@K$를 계산할 필요가 없으므로 이 경우 0을 반환하는 예외처리만 하면 됩니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def apk(actual, predicted, top_k):
if not actual:
return 0.0
if len(predicted) > top_k:
predicted = predicted[:top_k]
score, hits = 0, 0
for idx, item in enumerate(predicted):
if item in actual:
hits += 1
score += hits / (idx+1)
return score / min(len(actual), top_k)
나가며
사실 Average Precision 계열은 정의하는 방식이 여러 가지입니다. Precision-Recall Curve를 이용해서 계산하기도 하고, 본 포스트에서 제시한 방법대로 정의하기도 합니다. 물론 결과는 똑같지만, 아무 것도 모르는 상태에서는 오히려 이해에 독이 되기도 합니다. 그뿐만 아니라 Mean Average Precision은 추천 시스템에서 쓰기도 하고 Object Detection 분야에서도 쓰기 때문에 다른 메트릭에 비해서 헷갈리는 경우가 더 많은 듯합니다.
간혹 간과하지만, 메트릭에 대한 정의를 올바르게 알고 이해하는 것은 ML 문제를 구조화하고 해결하는 데에 큰 도움이 됩니다. 요즘에는 워낙 참고할만한 자료가 많아 메트릭에 대한 이해를 잘못하는 실수를 많이 줄일 수 있지만 메트릭 자체가 복잡하여 이해가 쉽지 않은 경우도 있죠. 그럴 때는 직접 구현해보거나 직접 예제를 만들어서 잘못된 것은 없는지 확인하는 것이 좋습니다.
Reference
[1] https://www.kaggle.com/competitions/h-and-m-personalized-fashion-recommendations/overview/evaluation
[2] https://cran.r-project.org/web/packages/recometrics/recometrics.pdf