Collaborative Denoising Auto-Encoders

Wu, Yao, et al. “Collaborative denoising auto-encoders for top-n recommender systems.” Proceedings of the ninth ACM international conference on web search and data mining. 2016.

들어가며

지난번 AutoRec 논문이 협업 필터링에 오토인코더를 도입한 논문이었다면, 오늘 다룰 Collaborative Denoising Auto-Encoder (CDAE) 논문은 오토인코더 대신 디노이징 오토인코더 (Denoising Auto-Encoder)를 도입한 논문입니다. 논문에서는 오토인코더 대신 디노이징 오토인코더를 사용함으로써 기존 협업 필터링 알고리즘들보다 높은 유연성을 가질 수 있다고 주장하는데요. 어떻게 디노이징 오토인코더를 협업 필터링에 녹여냈는지 한 번 살펴보도록 하겠습니다.

Problem Definition

논문에서는 다음의 notation을 사용합니다.

• 사용자 집합 $\mathcal{U} = { u = 1, \cdots, U }$
• 아이템 집합 $\mathcal{I} = { i = 1, \cdots, I }$
• 사용자의 과거 아이템 선호 로그 $\mathcal{O} = (u, i, y_{ui})$
• 관측되지 않았거나 결측값 집합 $\bar{\mathcal{O}}$
• $\mathcal{O}^\prime \subseteq \bar{\mathcal{O}}$

Denoising Auto-Encoders

일반적인 오토인코더는 입력값 $\mathbf{x} \in \mathbb{R}^D$를 히든 레이어를 태운 다음 $\hat{\mathbf{x}}$로 재구축하는 형태입니다. 디노이징 오토인코더는 입력값을 변조하여 히든 레이어에서 보다 강건한 피처를 찾을 수 있도록 합니다. 이런 입력값을 Corrupted input $\tilde{\mathbf{x}}$이라고 하는데요. 이 corrupted input은 가우시안 노이즈 (Gaussian noise)를 주거나 드롭아웃 (Drop-out)을 통해서 생성할 수 있습니다.

\[\begin{aligned} P(\tilde{\mathbf{x}}_d = \delta \mathbf{x}_d) &= 1-q \\ P(\tilde{\mathbf{x}} = 0) &= q \end{aligned}\]

이때 corruption을 편향되지 않도록 하기 위해서 $\delta = 1 / (1-q)$로 설정합니다. 본 포스트에서는 가우시안 노이즈보다는 드롭아웃을 중심으로 설명하도록 하겠습니다.

Proposed Methodology

Collaborative Denoising Auto-Encoder (CDAE)

Figure 1. A sample CDAE illustration for a user.

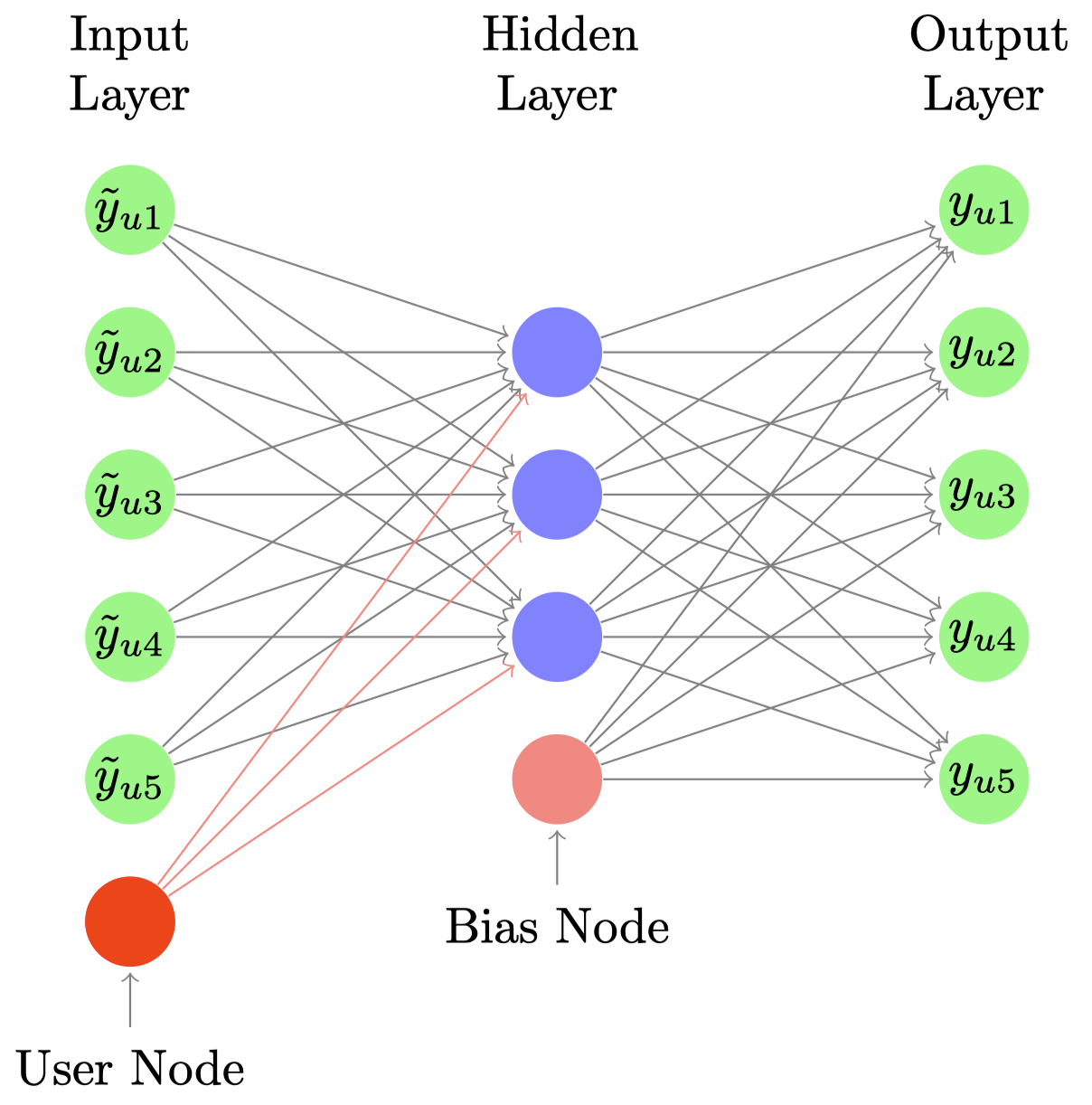
우선 일반적인 디노이징 오토인코더처럼 CDAE에서도 한 개의 히든 레이어를 가진 네트워크 구조를 사용합니다. 하나 기존 디노이징 오토인코더와 다른 부분은 인풋 레이어에서 사용자마다 하나의 노드를 추가로 받는다는 점입니다. 즉 사용자마다 $I+1$개의 노드를 갖게 되죠. $I$개의 노드는 사용자마다 전체 아이템에 대한 노드로 아이템 인풋 노드라고 부르고, 마지막 하나의 노드를 사용자 인풋 노드라고 부르도록 하겠습니다.

히든 레이어의 노드 수를 $K$ 라고 할 때, 아이템 인풋 노드와 히든 레이어 사이의 가중치를 $\mathbf{W} \in \mathbb{R}^{I \times K}$, 사용자 인풋 노드와 히든 레이어 사이의 가중치를 $\mathbf{V}_u \in \mathbb{R}^K$ 로 둘 수 있습니다. 히든 레이어와 아웃풋 레이어 사이의 가중치는 $\mathbf{W}^\prime \in \mathbb{R}^{I \times K}$ 가 되고, bias 노드에 대한 가중치는 $\mathbf{b} \in \mathbf{R}^I$ 가 됩니다.

CDAE는 우선 element-wise 함수 $h(\cdot)$ 에 대해서 다음을 통해 latent representations $\mathbf{z}_u$를 계산합니다. 이때 $h(\cdot)$ 은 identity function이나 sigmoid function을 사용합니다.

\[\mathbf{z}_u = h(\mathbf{W}^\top \tilde{\mathbf{y}}_u + \mathbf{V}_u + \mathbf{b}).\]

마지막으로 다음을 통해 히든 레이어에서 인풋 레이어를 재구축한 아웃풋 레이어를 계산합니다.

\[\hat{y}_{ui} = f \left({\mathbf{W}^\prime_i}^\top \mathbf{z}_u + \mathbf{b}_i^\prime \right)\]

CDAE의 파라미터는 reconstruction error를 최소화하여 학습합니다. L2 regularization을 포함한 다음의 loss 함수를 사용합니다.

\[\underset{\mathbf{W, W^\prime, V, b, b^\prime}}{\mathrm{argmin}} \frac{1}{U} \sum^U_{u=1} \mathbb{E}_{p(\tilde{\mathbf{y}}_u \mid \mathbf{y}_u)} \left[ \left( \tilde{\mathbf{y}}_u, \hat{\mathbf{y}}_u \right) \right] + \mathcal{R} \left( \mathbf{W, W^\prime, V, b, b^\prime} \right).\]

SGD와 AdaGrad를 이용해서 학습했으며 negative sampling을 사용했다고 합니다. 하지만 실제 구현할 때는 negative sampling을 굳이 사용할 필요가 없다고 생각합니다. 참고로 실제 검색을 통해 찾을 수 있는 많은 구현체에서도 거의 사용하지 않고 있습니다.

실제 CDAE를 이용해 아이템을 추천할 때는 사용자가 아직 액세스한 적이 없는 아이템만을 추천합니다. 위에서 정의한 notation을 따른다면 $\bar{\mathcal{O}}_u$ 에 있는 아이템만을 추천합니다.

자세한 실험 결과는 꽤 오래된 논문인만큼 본 포스트에서 굳이 다루지 않겠습니다.

Implementation

CDAE를 PyTorch로 구현하여 깃허브에 올려놓았습니다. AutoRec 때와 유사하게 GPU로 학습하고 구현에 사용한 설정값을 config 폴더에 저장해놓았습니다.

논문에서는 AdaGrad를 사용했지만 전 편의를 위해 Adam을 사용하였고, 별도의 regularzation을 하지 않도록 구성하였습니다. 또한 negative sampling을 사용하지 않았습니다.

마지막으로 평가 메트릭은 MAP@K만 구현해놓은 상태입니다. 다른 메트릭을 굳이 구현할 필요가 없어보여서 구현해놓지 않았는데 나중에 시간이 될 때 추가로 구현해놓고자 합니다.