Bayesian Personalized Ranking (BPR)
Rendle, Steffen, et al. “BPR: Bayesian personalized ranking from implicit feedback.” arXiv preprint arXiv:1205.2618 (2012).
Introduction
많은 추천 시스템 관련 교과서에서는 explicit rating을 이용하여 내용을 설명합니다. 하지만 대부분의 추천시스템들은 대부분 implicit feedback을 이용합니다. 클릭, 시청 시간 등의 implicit feedback은 사용자의 취향을 드러내지 않기 때문에 쉽게 수집 가능하기 때문이죠. 이 논문에서는 implicit feedback을 학습하는 추천 시스템을 Bayesian 관점에서 최적화하는 방법에 대해서 설명합니다.
Personalized Ranking
Implicit feedback으로 데이터를 구성하게 되면 positive한 관측치만 사용 가능합니다. 여기서 관측치는 사용자와 아이템의 조합입니다. 이 때 나머지 존재하지 않는 관측치는 negative feedback과 실제 결측치로 구성되어 있다는 점이 매우 중요합니다. 어떤 경우엔 정말로 해당 아이템이 마음에 들지 않았을 수 있지만 어떤 경우엔 해당 아이템의 존재 자체를 모를 수 있습니다. 이 두 가지 경우를 실제로 동일한 선상에서 negative하게 봐야하는가는 다시 생각해봐야 합니다. 본 논문에서는 이런 부분을 고려하여 새로운 접근법을 제시합니다.
Formalization
$U$를 전체 사용자의 집합, $I$를 전체 아이템의 집합이라고 했을 때 positive한 관측치 $s \in S \subseteq U \times I$로 나타낼 수 있습니다. 이제 사용자마다 개인화된 순위인 $>_u \subset I^2$를 구하는 것이 목표입니다. $>_u$는 다음의 특성을 갖고 있습니다.
Totality
\[\forall i, j \in I : i \neq j \implies i >_u j \ \vee \ j >_u i\]Anti-symmetry
\[\forall i, j \in I : i >_u j \ \wedge \ j >_u \implies i = j\]Transitivity
\[\forall i,j,k \in I : i >_u j \ \wedge j >_u k \implies i >_u k\]
편의를 위해서 다음을 정의합니다.
\[\begin{aligned} I_u^+ &:= \{ i \in I : (u, i) \in S \} \\ U_i^+ & := \{ u \in U : (u, i) \in S \} \end{aligned}\]Analysis of the problem setting
보통 추천 문제를 풀기 위해선 사용자마다 아이템의 선호도를 기반으로 개인화된 점수인 $\hat{x}_{ui}$를 예측하게 됩니다. 학습 데이터는 $(u, i) \in S$ 에서 positive class를, $(U \times I) \backslash S$ 에서 negative data를 추출하여 사용합니다. $S$에 포함된 데이터는 $1$로 예측하고 아닌 경우 $0$으로 예측하도록 학습합니다. 이런 접근법은 결측치와 실제 negative feedback을 하나로 간주하여 데이터를 구성하는 경우 사용자가 향후 관심을 가질 아이템을 무시하게 되는 문제가 있습니다.
이런 문제를 해결하기 위한 새로운 학습 데이터를 만들기 위해 다음의 가정을 세웁니다.
- 사용자 $u$가 아이템 $i_2$를 보았지만 아이템 $i_1$을 보지 않았다면 해당 사용자는 $i_1$보다 $i_2$를 선호함 : $i_2 >_u i_1$
- 사용자가 두 아이템을 모두 보았다면 어떤 아이템을 더 선호하는지 알 수 없음
- 사용자가 두 아이템을 모두 보지 않았다면 어떤 아이템을 더 선호하는지 알 수 없음

Figure 1은 위 가정들을 잘 설명하고 있습니다. 위 가정들을 토대로 새로운 학습 데이터 $D_S: U \times I \times I$를 다음과 같이 정의합니다.
\[D_S := \{ (u, i, j) \mid i \in I_u^+ \wedge j \in I \backslash I_u^+ \}\]$(u, i, j) \in D_S$는 사용자 $u$는 아이템 $j$보다 아이템 $i$를 더 선호한다는 의미이며, $i >_u j$ 입니다. 이 때 $>_u$는 anti-symmetric하므로 반대의 경우도 암묵적으로 포함하고 있습니다. 다시 말해서 $(u, i, j) \in D_S$ 라면 $(u, j, i) \not\in D_S$가 됩니다. 이렇게 순위에 기반을 둔 학습 데이터 정의는 다음의 장점을 갖습니다.
- 이 형태의 학습 데이터는 positive, negative, 결측값을 모두 포함합니다. 결측값은 예측 단계에서 순위가 매겨질 수 있는 사용자-아이템 쌍이 됩니다.
- 학습 데이터가 순위 자체를 목적으로 하여 생성됩니다.
Bayesian Personalized Ranking (BPR)
BPR Optimization Criterion
모든 아이템 $i \in I$에 대한 개인화한 순위를 찾기 위해 Bayesian을 이용하는 것은 주어진 모델의 파라미터 $\Theta$에 대해 다음의 사후 확률 (posterior probability)를 최대화하는 Maximum A Posteriori 문제로 생각할 수 있습니다.
\[p(\Theta \mid >_u) \propto p(>_u \mid \Theta) \ p(\Theta)\]Likelihood Function
이 때 모든 사용자들은 독립적으로 행동한다고 가정하고 모든 아이템쌍 역시 독립적이라고 가정합니다. 사용자 $u$에 대해서 아이템 $i, j$가 있다면 $>_u$는 두 가지 경우 $i >_u j$ 와 $j >_u i$ 만 존재합니다. 따라서 Bernoulli distribution을 따른다고 볼 수 있습니다. 위에서 모든 사용자와 모든 아이템쌍이 독립이라고 가정했으므로 i.i.d를 만족하므로 $b = (u, i, j) \in D_S$ 라고 했을 때 indicator function $\delta$에 대해 다음과 같이 쓸 수 있습니다.
\[\delta(b) \stackrel{\text{i.i.d}}{\sim} B(1, p(i >_u j))\]따라서 likelihood function $p(>_u \mid \Theta)$는 다음과 같이 쓸 수 있습니다.
\[\prod_{u \in U} p(>_u \mid \Theta) = \prod_{(u, i, j) \in U \times I \times I} p(i >_u j \mid \Theta)^{\delta((u, i, j) \in D_S)} \cdot (1-p(i>_uj \mid \Theta))^{\delta((u, j, i) \not\in D_S)}\]이 때 $>_u$는 totality와 anti-symmetry를 만족하기 때문에 전체 사용자에 대해서 모두 계산할 필요가 없습니다. $(u, i, j) \not\in D_S$ 여도 $(u, j, i) \in D_S$ 가 되기 때문입니다. 따라서 다음과 같이 간단하게 쓸 수 있습니다.
\[\prod_{u \in U} p(>_u \mid \Theta) = \prod_{(u, i, j) \in D_S} p(i >_u j \mid \Theta)\]이제 $p(i >_u j \mid \Theta)$에 대한 확률을 logistic sigmoid를 이용해 다음과 같이 정의합니다.
\[\sigma(x) := \frac{1}{1 + e^{-x}}\] \[p(i >_u j \mid \Theta) := \sigma(\hat{x}_{uij}(\Theta))\]$\hat{x}_{uij}(\Theta)$는 사용자 $u$, 아이템 $i$, 아이템 $j$ 사이의 관계를 설명하는 모델의 파라미터 벡터 $\Theta$에 대한 함수로 이 값을 얻기 위해 Matrix Factorization과 같은 모델을 학습합니다.
Prior Distribution
Prior $p(\Theta)$는 평균 $0$, 분산은 공분산 행렬 $\Sigma_\Theta$을 따르는 Normal distribution로 둡니다.
\[p(\Theta) \sim N(0, \Sigma_\Theta)\]이 때 계산의 간소화를 위해서 위 분포를 다음과 같이 계산합니다.
\[\begin{aligned} N(\Theta \mid 0, \Sigma_\Theta) &= \frac{1}{\sqrt{(2\pi)^d | \Sigma|}} e^{-\frac{1}{2} (\Theta^T \Sigma^{-1}\Theta)} \\ &\propto e^{-\frac{1}{2} (\Theta^T \Sigma^{-1}\Theta)}\\ & = e^{-\frac{1}{2\lambda_\Theta}\Theta^T \Theta} \\ &\approx e^{-\lambda_\Theta \Theta^T \Theta} \end{aligned}\]BPR-OPT
지금까지의 세팅으로 사후 확률 $p(\Theta \mid >_u)$를 최대화하기 위해 BPR-Opt를 계산하면 다음과 같습니다.
\[\begin{aligned} \text{BPR-Opt} &= \log p(\Theta \mid >_u) \\ &= \log p(>_u \mid \Theta) p(\Theta) \\ &= \log \prod_{(u,i,j) \in D_S} \sigma(\hat{x}_{uij}) p(\Theta) \\ &= \sum_{(u,i,j) \in D_S} \log \sigma(\hat{x}_{uij}) + \log p(\Theta) \\ &\approx \sum_{(u, i, j) \in D_S} \log \sigma(\hat{x}_{uij}) - \lambda_\Theta \| \Theta \|^2 \end{aligned}\]Analogies to AUC optimization
AUC와 BPR간 관련성을 보기 위해 AUC를 $(u,i,j) \in D_S$ 스키마로 정리해보도록 하겠습니다.
우선 사용자별 AUC는 다음과 같습니다.
\[\text{AUC}(u) := \frac{1}{|I_u^+| |I \backslash I_u^+|} \sum_{i \in I_u^+} \sum_{j \in I \backslash I_u^+} \delta(\hat{x}_{uij} > 0)\]위 식을 사용자에 대해 평균을 계산하면 평균 AUC를 얻을 수 있습니다.
\[\text{AUC} := \frac{1}{|U|} \sum_{u \in U} \text{AUC}(u)\]이걸 $(u, i, j) \in D_S$ 스키마로 다시 쓰면 다음과 같습니다.
\[\text{AUC}(u) = \sum_{(u, i, j) \in D_S} z_u \delta(\hat{x}_{uij} > 0)\]여기서 $z_u$는 normalizing constant 입니다.
\[z_u = \frac{1}{ |U| |I_u^+| |I \backslash I_u^+| }\]위 식을 보면 AUC와 BPR-Opt가 유사함을 알 수 있습니다. AUC는 미분이 불가능한 Heaviside function을 쓰고 BPR-opt는 미분 가능한 $\log \sigma(x)$를 쓰는 정도의 차이가 있습니다.
BPR Learning Algorithm
위에서 언급했듯 최적화를 해야하는 함수가 미분 가능하기 때문에 gradient descent를 이용해서 해당 criterion을 최적화합니다. 하지만 일반적인 gradient descent를 사용할 경우 문제가 있기 때문에 부트스트랩 샘플링을 활용한 gradient descent 방법인 LearnBPR을 도입합니다.
우선 모델 파라미터 $\Theta$에 대한 BPR-Opt의 그라디언트는 다음과 같습니다.
\[\begin{aligned} \frac{\partial \text{BPR-Opt}}{\partial \Theta} &= \sum_{(u, i, j) \in D_S} \frac{\partial}{\partial \Theta} \log \sigma(\hat{x}_{uij}) - \lambda_\Theta \frac{\partial}{\partial \Theta} \| \Theta \|^2 \\ &\propto \sum_{(u, i, j) \in D_S} \frac{-e^{\hat{x}_{uij}}}{1 + e^{-\hat{x}_{uij}}} \cdot \frac{\partial}{\partial \Theta} \hat{x}_{uij} - \lambda_\Theta \Theta \end{aligned}\]이 그라디언트를 이용해 최적화하는 gradient descent는 크게 full gradient descent와 stochastic gradient descent로 나눌 수 있습니다.
- Full Gradient Descent
- \[\Theta \leftarrow \Theta - \alpha \frac{\partial \text{BPR-Opt}}{\partial \Theta}\]
- 전체 데이터에 대한 그라디언트를 계산하기 때문에 올바른 방향으로 수렴하기는 하나 속도가 너무 느립니다.
- $O(\vert {S}\vert \vert{I}\vert)$ 만큼 계산을 해야 하기 때문에 실제 full gradient를 이용해 업데이트하는 것은 어려움이 따릅니다.
- 학습 데이터의 형태로 인해 학습에 편향이 발생하여 (the skewness in the training pairs) 수렴이 어려워집니다.
- 일반적으로 사용자 $u$에 대해 positive한 아이템 $i$는 negative한 아이템 $j$보다 그 수가 많기 때문에 아이템 $i$는 손실 함수에서 더 큰 영향력을 갖습니다.
- 따라서 $i$에 종속적인 모델 파라미터의 그라디언트가 전체 그라디언트를 지배하게 됩니다.
- 이는 결국 매우 작은 learning rate를 선택하게 만듭니다.
- 그라디언트들이 너무 다르기 때문에 regularization이 어렵습니다.
- Stochastic Gradeint Descent
- \[\Theta \leftarrow \Theta + \alpha \left(\frac{e^{\hat{x}_{uij}}}{1 + e^{-\hat{x}_{uij}}} \cdot \frac{\partial}{\partial \Theta} \hat{x}_{uij} + \lambda_\Theta \Theta \right)\]
- 학습 데이터 내의 개별 인스턴스의 그라디언트를 계산해서 업데이트 합니다.
- 위에서 언급한 학습에서의 편향성 문제를 해결하기엔 좋은 방법이나 학습 데이터 쌍을 어떤 순서로 탐색하느냐가 매우 중요합니다.
- 일반적으로는 사용자 단위나 아이템 단위로 데이터를 탐색하지만 수렴이 잘 이루어지지 않습니다.
- 연속적으로 존재하는 동일한 사용자-아이템 순서쌍을 계속 업데이트하는 경우가 발생하기 때문입니다.
따라서 본 논문에서는 stochastic gradient descent를 사용하되 학습 데이터 내의 개별 인스턴스들을 uniformly distributed하게 샘플링하여 그라디언트를 계산하여 업데이트합니다. 또한 일반적인 샘플링보다는 복원 추출하는 부트스트랩 샘플링을 권장합니다.

실제로 이런 방식을 사용했을 때 훨씬 빠르게 수렴할 뿐만 아니라 성능도 더 좋은 것을 확인할 수 있습니다.
Learning models with BPR
우선 $(u, i, j) \in D_S$에 대해서 최적화하기 위해 $\hat{x}_{uij}$를 다음과 같이 분해합니다.
\[\hat{x}_{uij} := \hat{x}_{ui} - \hat{x}_{uj}\]이 때 $\hat{x}_{ui}$ 같은 단일 스코어를 예측하도록 하는 것이 아닌 두 예측값의 차이를 분류하는 형태를 다루게 됩니다.
Matrix Factorization
Matrix Factorization에서는 행렬 $X : U \times I$를 두 개의 low-rank 행렬의 곱을 통해 근사하여 값을 예측합니다.
\[W : |U| \times k, \quad H : |I| \times k \implies \hat{X} := W H^T\]모델의 예측값은 다음과 같습니다.
\[\hat{x}_{ui} = \langle w_u, h_i \rangle = \sum^k_{f=1} w_{uf} \cdot h_{if}\]이 때 모델 파라미터는 $\Theta = (W, H)$ 이므로 BPR-Opt는 다음과 같습니다.
\[\begin{aligned} \text{BPR-Opt} = \log p(\Theta \mid >_u) &= \sum_{(u, i, j) \in D_S} \log \sigma(\hat{x}_{uij}) - \lambda_\Theta \| \Theta \|^2 \\ &= \sum_{(u, i, j) \in D_S} \log \sigma(\hat{x}_{uij}) - \lambda_{W} \| \mathbf{w}_u \|^2 - \lambda_{H^+} \|\mathbf{h}_i\|^2 - \lambda_{H^-} \| \mathbf{h}_j\|^2 \end{aligned}\]또한 \(\hat{x}_{uij} = \hat{x}_{ui} - \hat{x}_{uj}\) 이므로 다음이 성립합니다.
\[\hat{x}_{uij} = \sum w_{uf} \cdot h_{if} - \sum w_{uf} \cdot h_{jf}\]따라서 $\hat{x}_{uij}$의 그라디언트는 다음과 같습니다.
\[\frac{\partial}{\partial \theta} \hat{x}_{uij} = \begin{cases} (h_{ij} - h_{jf}) & \text{if } \theta = w_{uf}, \\ w_{uf} & \text{if } \theta = h_{if}, \\ -w_{uf} & \text{if } \theta = h_{jf}, \\ 0 & \text{else} \end{cases}\]Evaluation
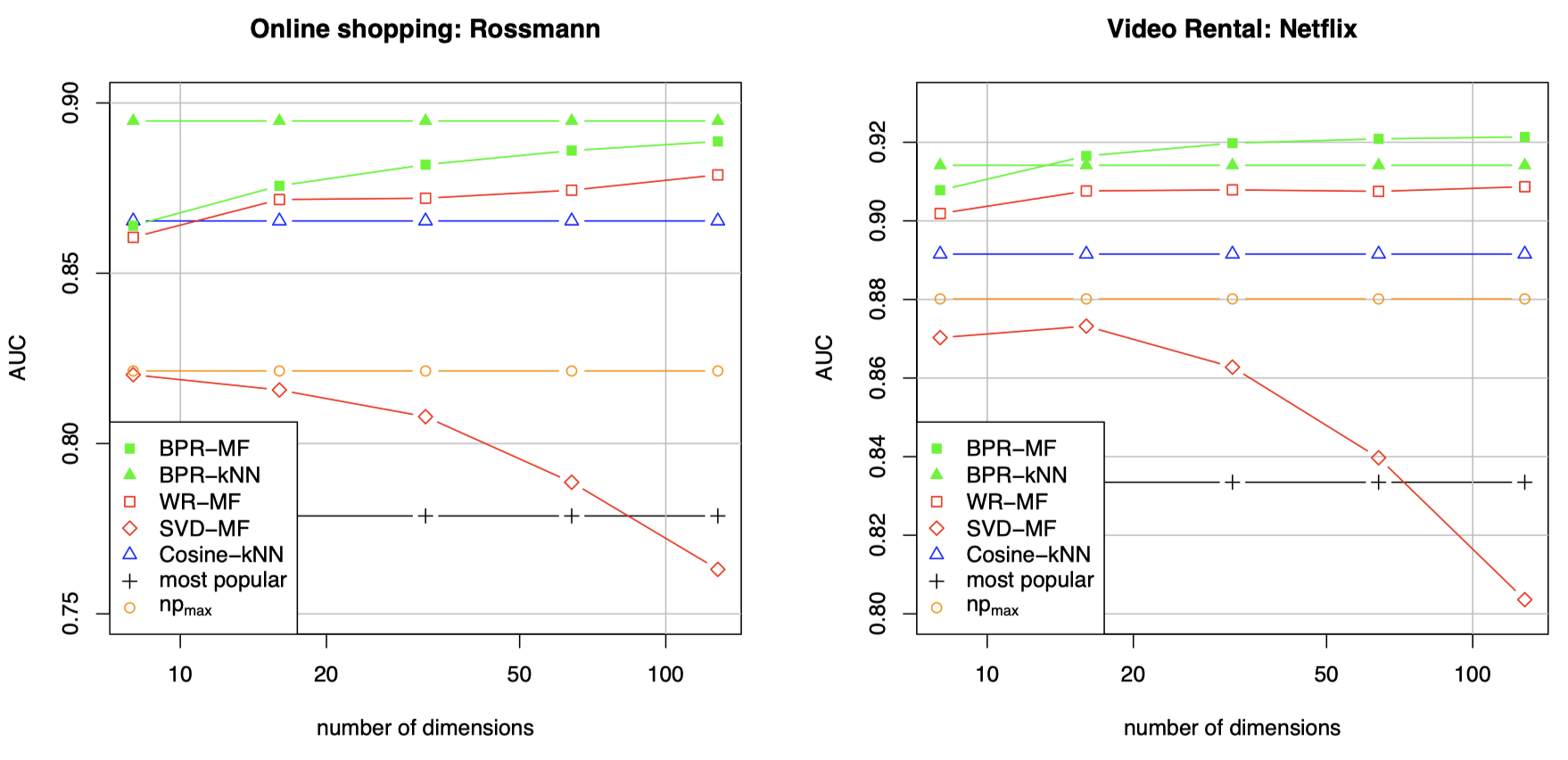
대부분의 설정값에서 AUC 기준 BPR의 성능이 더 좋은 것을 확인할 수 있습니다.
Conclusion
BPR은 높은 성능을 보이며 최근 implicit feedback을 학습하는 추천 알고리즘들 그리고 오픈소스들에서 널리 쓰이고 있습니다. 당장에 유명한 오픈소스인 LightFM, Implicit 등에서도 BPR을 지원하고 있습니다. BPR 외에 implicit feedback을 학습할 때 사용하는 손실 함수는 WARP 가 있습니다. 두 개의 차이가 있다면 BPR은 AUC와 밀접한 관련이 있고 WARP는 NDCG를 최적화하는 느낌이 있습니다. 일반적으로는 WARP가 더 나은 성능을 보인다는 이야기가 있으나 구현되어 있는 오픈소스가 많지 않아 아직까지는 BPR이 많이 쓰이는 듯 합니다. WARP는 기회가 되면 정리하여 포스팅해보도록 하겠습니다.