Neural Collaborative Filtering
He, X., Liao, L., Zhang, H., Nie, L., Hu, X., & Chua, T. S. (2017, April). Neural collaborative filtering. In Proceedings of the 26th international conference on world wide web (pp. 173-182).
Background
Matrix Factorization(MF) 는 Netflix Prize로 인해 유명해졌습니다. 하지만 사용자와 아이템의 상호작용을 내적(inner product) 한다는 점이 문제였습니다. 상호작용의 계산이 너무 선형적이어서 복잡한 구조의 상호작용을 표현하기엔 어려움이 있었죠.
그래서 이 논문에선 상호작용을 학습하기 위해 DNN을 사용합니다. 논문 발표 이전 시점의 연구들이 아이템에 대한 텍스트 데이터, 오디오 피쳐, 이미지의 시각적 콘텐츠 같은 다소 부수적인 정보에 대해 DNN을 사용했던 것과는 대조적입니다. 또한 implicit feedback에 더 초점을 맞추어 DNN으로 노이즈가 많은 implicit feedback을 어떻게 모델링하는지에 대해 살펴봅니다.
Preliminary
Learning from Implicit Data
먼저 사용자의 implicit feedback으로부터 사용자-아이템 상호작용 행렬 $\mathbf{Y} \in \mathbb{R}^{M \times N}$을 정의합니다.
\[y_{ui} = \begin{cases} 1, \quad \text{if interaction (user $u$, item $i$) is observed;} \\ 0, \quad \text{otherwise.} \end{cases}\]$y_{ui} = 1$ 이더라도 사용자 $u$가 아이템 $i$를 좋아한다는 의미는 아닙니다. 반대로 $y_{ui} = 0$ 이더라도 싫어한다는 의미가 아니죠. 단순히 해당 사용자는 그 아이템을 인식하지 못했을 뿐입니다. 이런 점이 implicit feedback 을 모델링하기 어렵게 만듭니다.
Implicit feedback을 학습하는 추천 문제는 아직 접하지 않은 아이템에 대한 점수를 추정하는 작업입니다. 이 때, 아이템에 대한 점수는 아이템의 순위로 사용됩니다. 사용자 $u$가 아이템 $i$에 대한 점수는 $\hat{y}_{ui} = f(u , i \mid \Theta)$ 로 나타낼 수 있습니다.
- $\Theta$ : 모델 파라미터
- $f$ : 모델 파라미터와 예측 점수를 매핑해주는 함수 (논문에선 interaction function으로 표현합니다.)
이런 문제를 해결할 때 사용하는 목적 함수의 형태는 크게 Pointwise loss와 Pairwise loss로 구분합니다. Pointwise loss는 Explicit feedback에 사용하기 편한데, Regression 프레임워크처럼 예측값과 타겟값의 차이를 최소화하는 방향으로 학습하게 됩니다. Pairwise loss는 사용자가 접한 아이템은 반드시 접하지 않은 아이템보다 높은 순위일 것이라는 가정으로 학습하게 됩니다. 따라서 사용자가 접한 아이템과 접하지 않은 아이템의 점수 간극을 넓히는 방향으로 학습하게 됩니다. NCF 프레임워크에서는 두 가지 학습 방식을 다 지원한다고 합니다.
Matrix Factorization
사용자와 아이템에 대한 latent vector의 내적으로 $y_{ui}$ 를 추정합니다. Latent vector의 차원 수를 $K$ 라고 할 때 다음과 같이 $y_{ui}$ 를 추정합니다. 사용자와 아이템의 latent factor를 각각 $\mathbf{p}_u, \mathbf{q}_i$로 둘 때 다음과 같습니다.
\[\hat{y}_{ui} = f(u, i \mid \mathbf{p}_u, \mathbf{q}_i) = \mathbf{p}_u^T \mathbf{q}_i = \sum^k_{k=1} p_{uk} q_{ik}.\]MF 모델은 latent space의 각 차원이 서로 독립이며 동일한 가중치로 선형 결합을 하는 것으로 가정합니다. 따라서 MF를 latent factor들의 선형 모델로 생각할 수 있습니다.
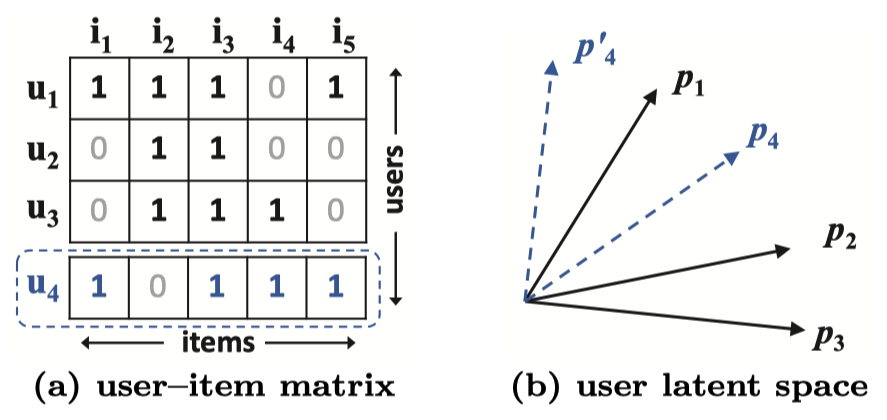
하지만 복잡한 사용자-아이템 상호작용을 저차원의 latent space로 추정하는 것은 한계가 명확합니다. Figure 1이 그 한계점을 보여줍니다. 자카드 유사도 (Jaccard similarity)로 계산한 $u_1, u_2, u_3$ 를 2차원 latent space에 표현하면 (b)의 그림처럼 됩니다. 세 명의 사용자까지는 충분히 표현이 가능하게 됩니다.
하지만 $u_4$ 에 대해서는 다릅니다. 자카드 유사도를 계산하면 $s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2)$ 입니다. 하지만 이 관계를 2차원의 latent space에는 표현할 수 없습니다. 이런 문제를 해결하기 위해선 고차원의 latent space를 활용하면 되지만, 모델의 일반화 측면에서 과적합이 발생하는 등의 문제를 야기합니다. 본 논문에서는 DNN을 통한 학습으로 이 문제를 해결하였다고 합니다.
Neural Collaborative Filtering
General Framework
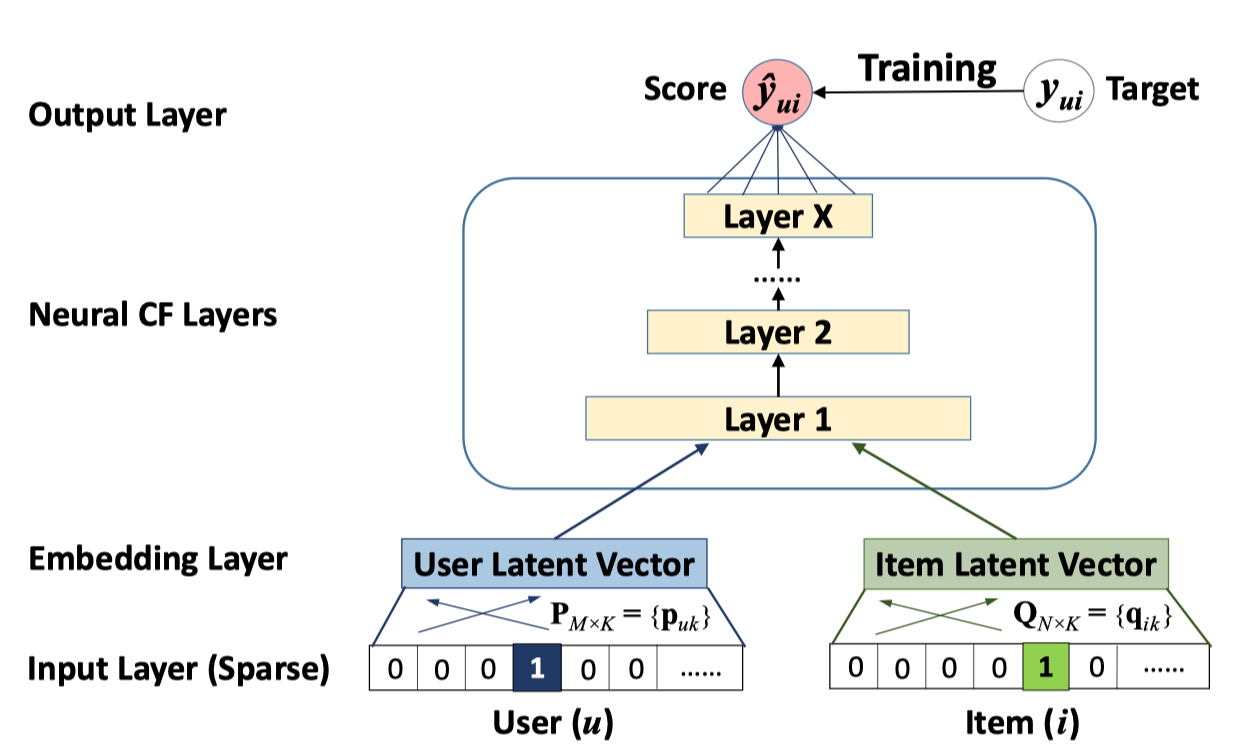
Collaborative filtering에 뉴럴 네트워크를 적용하기 위해 Figure 2처럼 사용자-아이템 상호작용 $y_{ui}$ 를 모델링하는 멀티 레이어 수조를 제안합니다.
- 인풋 레이어는 각각 사용자와 아이템을 표현하는 벡터들인 $\mathbf{v}_u^U, \mathbf{v}_i^I$ 로 구성됩니다.
- One-hot encoding을 통해 sparse한 binarized vector를 사용합니다.
- Cold-start problem을 해결하기 위해 컨텐츠 피처들을 사용하는 것도 방법이라고 합니다.
- 인풋 레이어 위에는 sparse representation을 dense vector로 바꿔주는 임베딩 레이어가 있습니다.
- 각각의 임베딩 레이어는 일종의 latent vector로 볼 수 있습니다.
- 각각의 임베딩 레이어는 멀티 레이어 뉴럴넷 구조로 들어가게 됩니다.
- 이 구조를 저자들은 neural collaboriative filtering layers (Neural CF Layers)로 부릅니다.
- \(\hat{y}_{ui}\) 와 타겟값인 $y_{ui}$ 사이의 pointwise loss를 최소화하는 방향으로 학습을 수행합니다.
- Bayesian Personalized Ranking (BPR)과 같은 pairwise loss도 사용 가능합니다.
Learning NCF
모델 파라미터를 학습하기 위해 pointwise loss를 최소화할 때 일반적인 squared loss를 사용할 수 있으나, implicit feedback에 대해서는 사용하기 어렵습니다. 따라서 아웃풋 레이어 $\phi_{out}$ 에 Logistic function이나 Probit function을 사용해 $\hat{y}_{ui} \in [0, 1]$ 과 같은 확률적 표현이 가능하도록 해야합니다. 위 설정에서 likelihood function은 아래와 같습니다.
\[p(\mathcal{Y}, \mathcal{Y}^- \mid \mathbf{P}, \mathbf{Q}, \Theta_f) = \prod_{(u, i) \in \mathcal{Y}} \hat{y}_{ui} \prod_{(u, j) \in \mathcal{Y}^-} (1 - \hat{y}_{uj}).\]- $\mathcal{Y}$ : 상호작용이 있는 데이터
- $\mathcal{Y}^-$ : 상호작용이 없는 데이터 (the set of negative instances)
그 후 negative logarithm을 취하면 일반적인 binary cross-entropy loss와 같아지며, SGD를 이용해 최적화할 수 있습니다.
\[\begin{aligned} L &= - \sum_{(u, i) \in \mathcal{Y}} \log \hat{y}_{ui} - \sum_{(u, j) \in \mathcal{Y}^-} \log (1 - \hat{y}_{uj}) \\ & = -\sum_{(u, i) \in \mathcal{Y} \cup \mathcal{Y}^-} y_{ui} \log \hat{y}_{ui} + (1 - y_{ui}) \log(1 - \hat{y}_{ui}). \end{aligned}\]이 때 $\mathcal{Y}^-$ 는 매 학습 반복 (iteration) 시 negative sampling을 통해 생성할 수 있습니다. 샘플링 비율은 $\mathcal{Y}$ 의 크기에 비례하여 설정할 수 있습니다.
Generalized Matrix Factorization (GMF)
NCF 프레임워크에서 MF는 일부 차이점을 제외하곤 비슷합니다. 차이점은 아래와 같습니다.
내적이 아닌 element-wise product를 합니다.
\[\hat{y}_{ui} = a_{out} (\mathbf{h}^T (\mathbf{p}_u \ \odot \ \mathbf{q}_i))\]Edge weight인 $\mathbf{h}$ 에서 uniform constraint를 제외하면 latent space의 각 차원에 중요도를 다르게 할 수 있습니다.
- 논문에서는 sigmoid function을 사용했습니다.
Activation function인 $a_{out}$ 을 비선형 함수로 선정하면 기존 선형 MF 모델보다 더 풍부한 표현이 가능합니다.
- 논문에서는 logloss 를 사용했습니다.
Multi-Layer Perceptron (MLP)
NCF는 사용자와 아이템에 대해 모델링을 수행하기 때문에, 각 피처를 concatenate하는 것이 직관적입니다. 여기에 사용자와 아이템의 latent feature 사이의 상호작용을 학습하기 위해 히든 레이어를 추가한 일반적인 MLP를 사용합니다.
Activation function으로는 ReLU가 경험적으로 더 좋은 성능을 냈으며, 다음 히든 레이어가 이전 히든 레이어의 절반 크기가 되도록 타워 구조를 사용했습니다.
Fusion of GMF and MLP
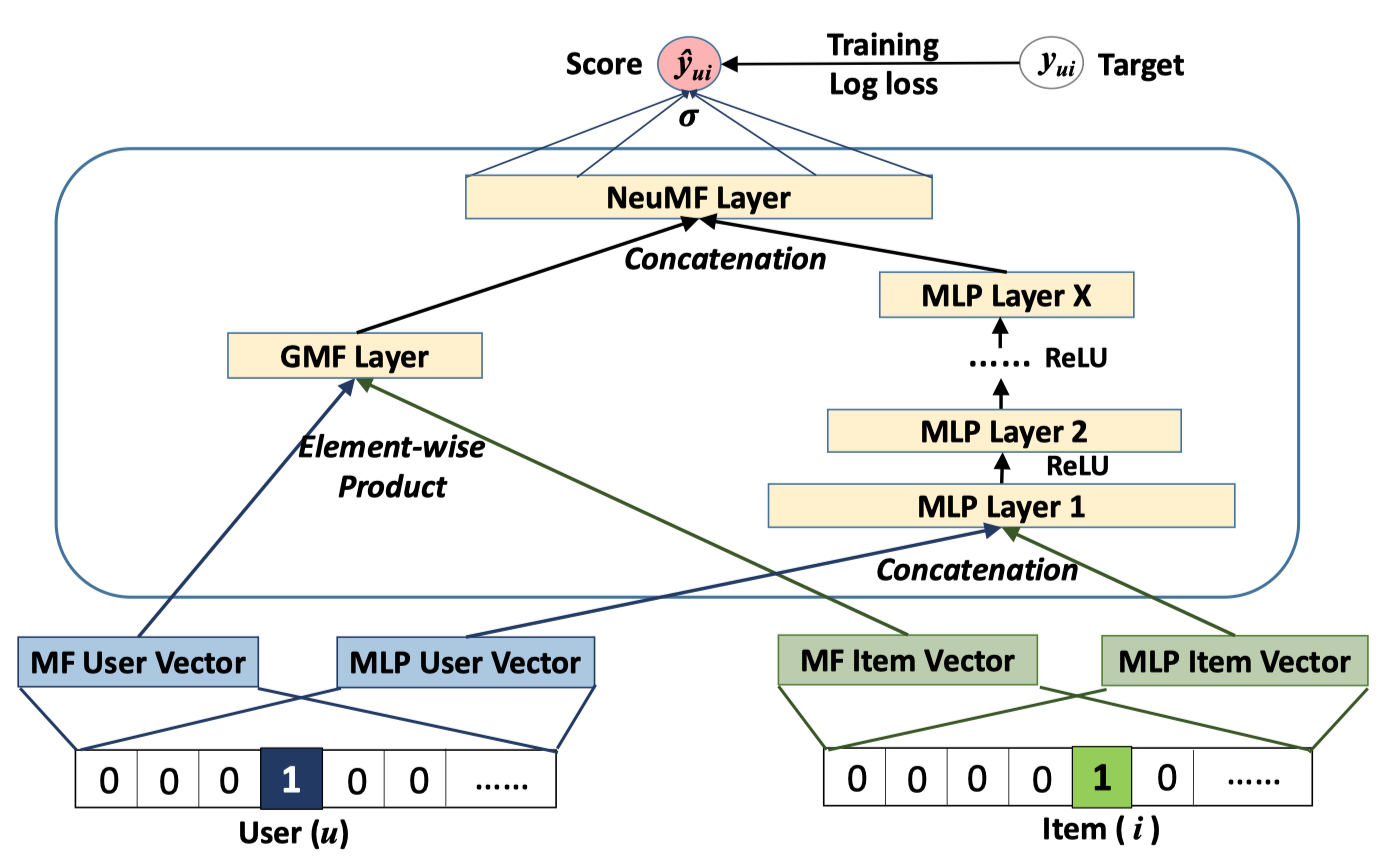
NCF 프레임워크에서 GMF와 MLP가 모두 복잡한 상호작용을 잘 학습할 수 있게 하기 위해선 각각의 임베딩 레이어를 공유하고, 그 아웃풋을 합치는 것입니다. 하지만 동일한 크기의 임베딩 레이어를 사용하는 것은 문제가 될 수 있습니다. 각 서브 모델들의 최적 임베딩 크기가 다르기 때문입니다. 따라서 저자들은 서브 모델들이 각각의 임베딩을 사용하게 하고, 마지막 히든 레이어에서 두 서브 모델을 concatenate 하는 방식을 Figure 3처럼 제안합니다. 이 모델 구조를 Neural Matrix Factorization (NeuMF)로 부릅니다.
Pre-training
논문에선 본 모델에 대해 pre-trained 구조를 사용한다고 합니다. 저자들은 GMF와 MLP에 대해 다음의 방식을 제안합니다.
- GMF와 MLP를 랜덤 초기화하여 수렴할 때까지 학습합니다.
- 훈련된 모델의 파라미터를 NeuMF의 파라미터로 사용합니다.
- 마지막 아웃풋 레이어에서 두 모델을 concatenate할 때 가중치를 부여합니다.
- Optimizer로 Adam을 사용합니다.
Experiments
다음의 세 개의 목적에 맞는 각각의 실험 결과를 살펴봅니다.
- RQ1 : SOTA 수준의 결과인가?
- RQ2 : Negative sampling을 사용한 logloss 등 제안한 최적화 프레임워크가 효과적인가?
- RQ3 : 더 많은 수의 히든 레이어가 도움되는가?
Performance Comparison (RQ1)
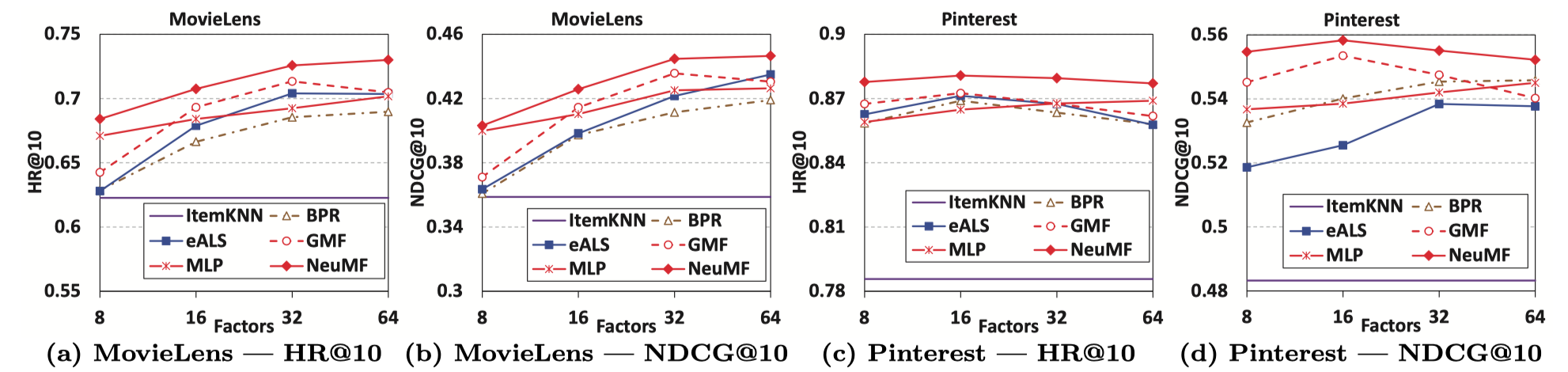
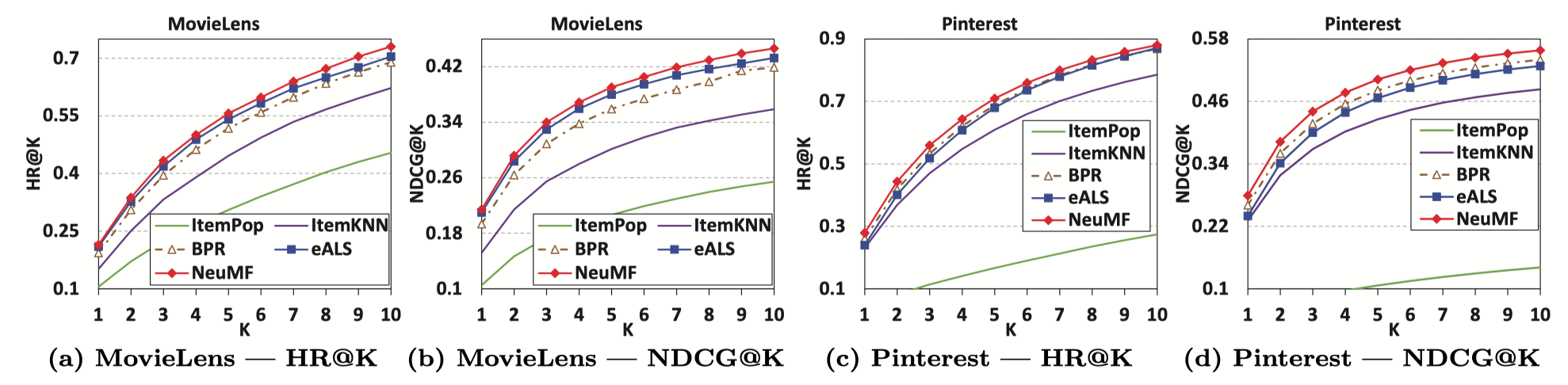
당시 다른 모델들에 비해 더 나은 성능을 보입니다. 또한 논문에선 pre-training 후에 더 높은 성능을 보였다고 말합니다.
Log Loss with Negative Sampling (RQ2)
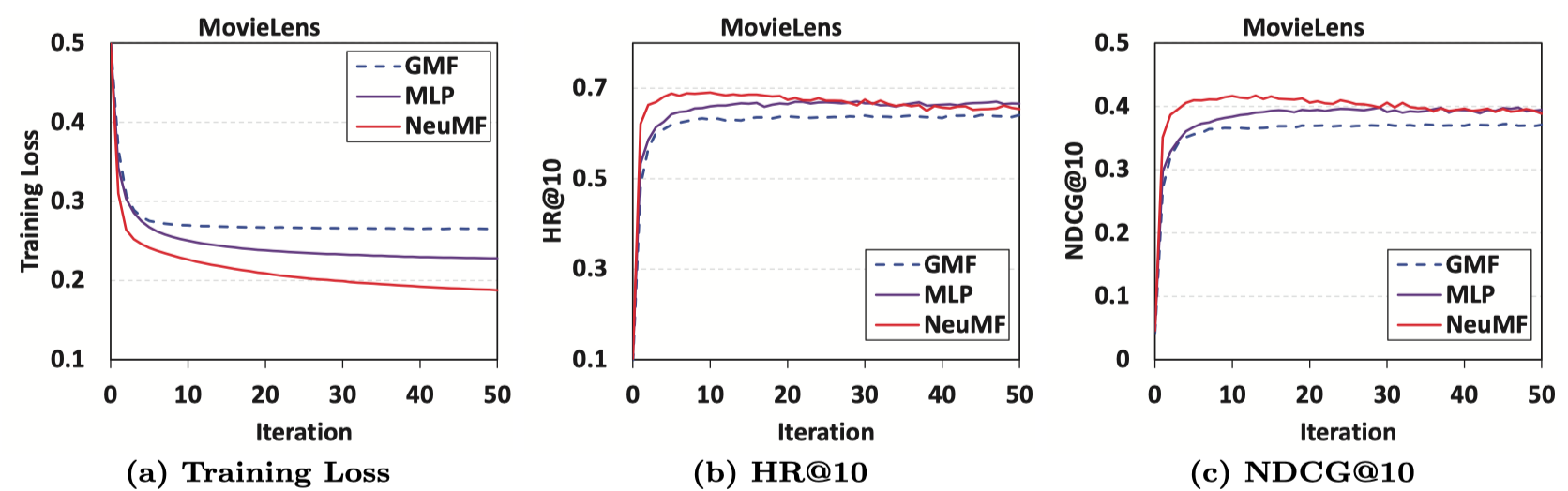

실험 결과를 보면 적은 Iteration에서 최적의 성능을 내며 그 이후 성능이 감소하는 것을 확인할 수 있습니다. 그리고 NeuMF가 GMF와 MLP보다 나은 성능을 보입니다. Negative sampling은 적정 수를 사용하였을 때 더 나은 성능을 보였습니다.
Is Deep Learning Helpful? (RQ3)
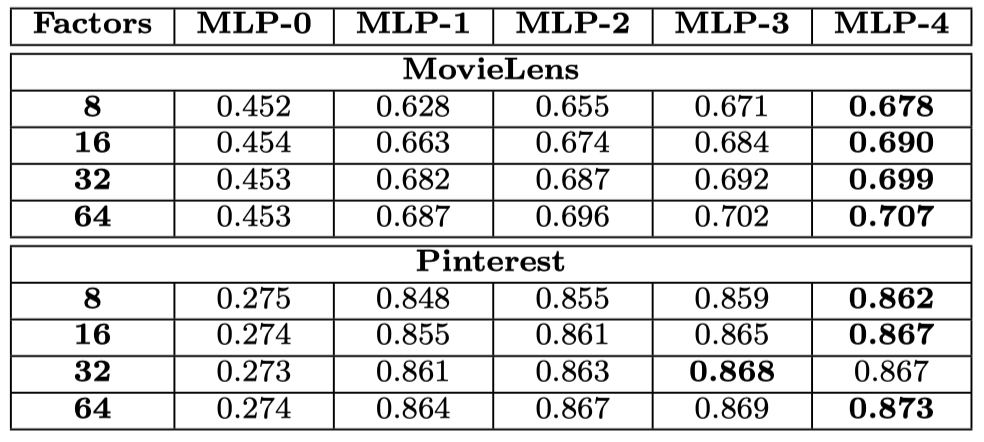
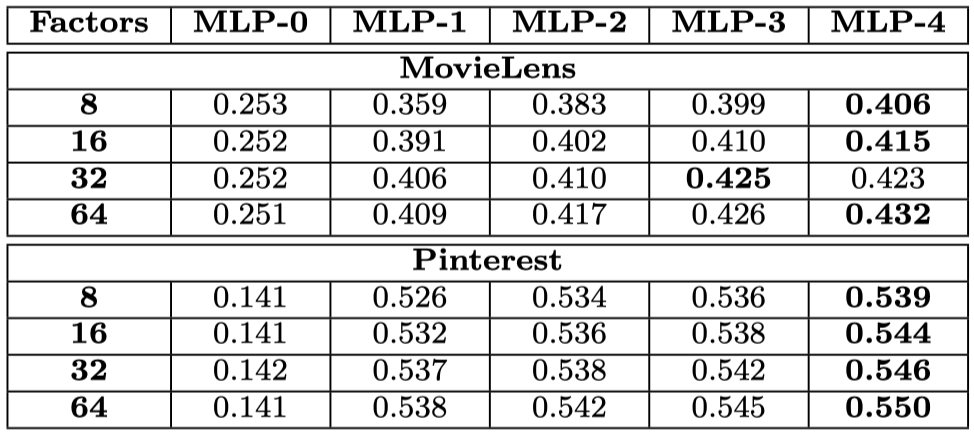
더 깊은 구조가 전반적으로 좋은 성능을 내고 있습니다.