Multi-armed Bandit
A/B 테스트를 대체할 수 있는 Multi-armed Bandit에 대해서 알아봅시다. 🎰
들어가며
두 개 이상의 다른 광고, 추천 알고리즘 결과 등의 성능을 비교하여 평가할 때 A/B 테스트를 많이 사용합니다. 기존의 제품과 새로 만든 제품을 각각 대조군과 실험군으로 설정하여 어떤 제품이 더 나은지 통계적으로 검증합니다.

온라인 광고에 A/B 테스트를 적용하는 것을 한번 생각해보죠. 두 개의 광고가 있다면, 전체 사용자를 적당한 기준을 두어 두 개의 그룹으로 나눕니다. 두 그룹의 기존 트래픽이 큰 차이가 나지 않도록 나누어 서로 다른 광고를 보여줍니다. 그리고 어떤 광고의 전환율(conversion rate)이 통계적으로 유의한 수준에서 더 나은지 확인합니다. 이 방법은 매우 직관적이며 구현도 쉽습니다.
하지만 A/B 테스트는 다음과 같은 문제가 있습니다.
- 충분한 샘플이 모일 때까지 각 그룹의 트래픽을 동일하게 할당하게 되는데, 중간에 그 트래픽을 재할당하는 것이 불가능합니다.
- 이 경우 통계적으로 유의미한 결과가 나올 때까지 A/B 테스트를 유지해야 하며, 이때 비용 관점에서 매우 큰 손실이 발생할 수 있습니다.
- 실험군의 퍼포먼스가 좋지 못하면 문제가 더 커집니다.
- 특정 그룹에서의 퍼포먼스가 좋지 않음에도 불구하고 해당 테스트를 계속해서 유지해야 하기 때문입니다.
- 해당 그룹의 사용자들은 계속 안 좋은 제품이나 서비스를 받게 되고, 더 나아가 사용자 이탈까지 발생할 수도 있습니다.
이러한 문제점을 전체적으로 해결할 방법이 바로 Multi-armed Bandit (MAB)입니다.
Multi-armed Bandit

Multi-armed bandit은 사전적으론 ‘팔이 여러 개인 도적’이란 뜻입니다. 사진에 있는 하나의 슬롯머신을 One-armed bandit이라고 부르는 데에서 착안한 이름입니다.
슬롯머신이 하나가 아니라 여러 개가 있을 때 각 슬롯머신은 서로 다른 승리 확률을 갖고 있습니다. Multi-armed bandit은 여러 개의 슬롯머신이 있을 때 가장 많은 보상을 얻을 방법에 대한 문제를 해결하는 것입니다.
Exploration / Exploitation
어떤 슬롯머신이 나에게 가장 많은 돈을 벌어다 줄지는 모르기 때문에 결국 모든 슬롯머신을 다 돌려봐야 합니다. 그렇게 각 슬롯머신을 몇 번 돌리고 나면 승률이 높은 슬롯머신을 파악하게 되고, 그 슬롯머신을 돌려서 돈을 벌게 됩니다. 하지만 승률이 높은 슬롯머신이 정말 제일 승률이 높은지 확신할 수 없기 때문에 추가적인 정보가 필요하겠죠. 결국 다른 슬롯머신을 몇 번은 더 돌려봐서 지금까지의 데이터를 더 정밀하게 업데이트 해야 합니다.
이처럼 슬롯머신을 돌려서 승률을 확인하는 것을 Exploration(탐색), 가장 높은 승률을 가진 것으로 예상되는 슬롯머신을 이용해 보상을 얻는 것을 Exploitation(수확)이라고 합니다. 이 두 가지는 Multi-armed Bandit에서 모두 이루어지며, 그 밸런스를 적절하게 조절해야만 합니다. 이를 Exploration and Exploitation Trade-off 라고 합니다.
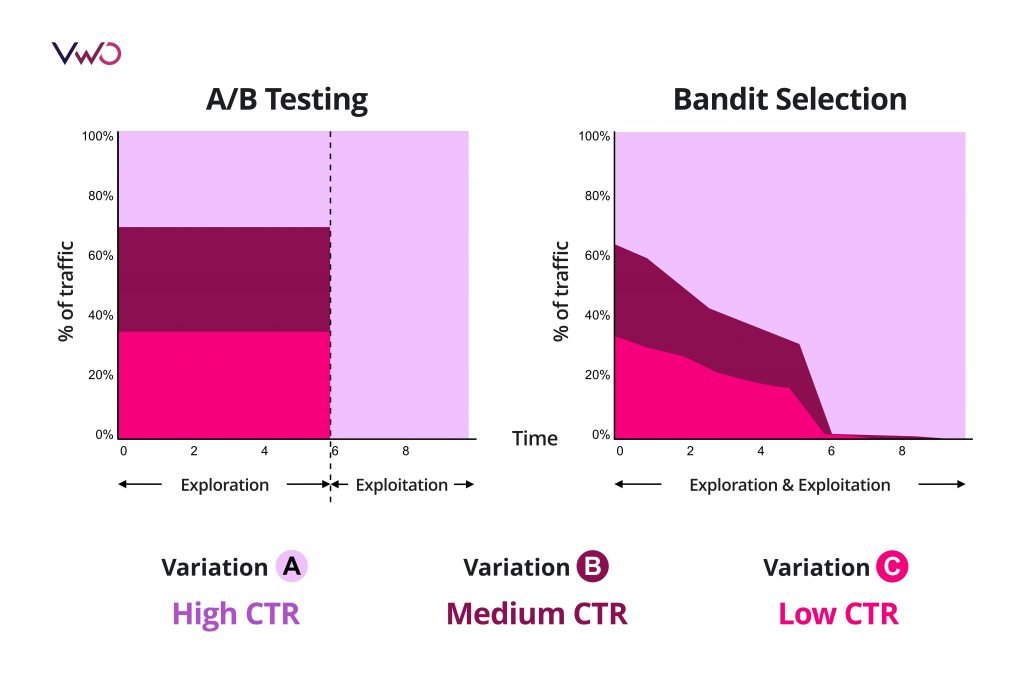
사실 A/B 테스트 역시 Exploration and Exploitation Trade-off를 갖습니다. 각 그룹에 대해 통계적으로 유의한 정도의 샘플을 얻는 과정이 Exploration이고, 여기서 가장 좋은 결과가 나온 케이스를 반영하는 것이 Exploitation이죠. 하지만 A/B 테스트는 위에서 언급한 것처럼 Exploration에서 발생하는 비용이 너무 큽니다. 하지만 MAB는 Exploration과 Exploitation을 계속해서 조정할 수 있기 때문에 그 비용을 줄일 수 있습니다.
알고리즘
MAB 문제를 해결하는 알고리즘은 매우 다양합니다. 그중에서 중요한 알고리즘 몇 개를 간단하지만 퍼포먼스가 낮은 알고리즘부터 복잡하지만 퍼포먼스가 좋은 알고리즘 순서대로 알아보도록 하겠습니다.
$\varepsilon$-greedy
$\varepsilon$-greedy 알고리즘은 제일 기본적인 알고리즘입니다. Exploration과 Exploitation을 조절할 파라미터인 $\varepsilon$을 도입합니다. 이 때 $\varepsilon$은 0과 1 사이의 값입니다.
- $1-\varepsilon$의 확률로 지금까지 관측한 슬롯머신 중에서 가장 많은 보상을 주는 슬롯머신을 선택합니다. (Exploitation)
- $\varepsilon$의 확률로 나머지 슬롯머신 중 하나의 슬롯머신을 선택하여 탐색합니다. (Exploration)
간단하게 $\varepsilon$의 값이 커질수록 탐색의 비중이 높아지고, 값이 낮을수록 지금까지 가장 큰 보상을 준 슬롯머신만을 선택하는 확률이 높아집니다. 매우 직관적이고 간단한 알고리즘인 만큼 그 결과가 우수하진 않습니다. $\varepsilon$-greedy 알고리즘의 단점은 다음과 같습니다.
- 최적의 슬롯머신을 찾았다고 하더라도 $\varepsilon$의 확률로 불필요한 탐색을 계속하게 됩니다.
- 슬롯머신에 대한 탐색이 임의로 이루어지기 때문에 특정 슬롯머신에 대해서는 충분한 정보를 얻지 못할 수도 있습니다.
Softmax
$\varepsilon$-greedy 알고리즘으로 MAB 문제를 해결한다고 할 때 다음의 두 시나리오를 한 번 생각해보겠습니다.
- Scenario A : 각 슬롯머신에서 얻을 수 있는 돈의 차이가 크지 않음
- Scenario B : 각 슬롯머신에서 얻을 수 있은 돈의 차이가 큼
$\varepsilon$-greedy 알고리즘은 두 시나리오에 대해 각 슬롯머신을 동일한 확률인 $\varepsilon$으로 탐색합니다. 하지만 벌 수 있는 돈의 차이가 크다면 돈을 벌 수 있는 슬롯머신을 선택할 확률을 차이에 비례하여 높이고 싶은 것이 당연합니다.
각 슬롯머신에 대한 보상 확률을 Softmax로 변환하여 이 문제를 해결할 수 있습니다.
\[P(i) = \dfrac{e^{r_i / \tau}}{\sum e^{r_k / \tau}} \label{eq1}\tag{1}\]- $r_i$ : 현재까지의 슬롯머신 $i$의 평균 선택 확률
- $\tau$ : 확률 조정에 대한 하이퍼 파라미터 (Temperature)
각 슬롯머신 $i$에 대한 Softmax 확률값인 $P(i)$를 $\varepsilon$-greedy 알고리즘처럼 수행하면 됩니다.
여기서 확률을 조정하는 파라미터인 $\tau$에 대해서 더 자세히 알아보도록 하겠습니다. $\eqref{eq1}$ 에서 우변을 $e^\frac{r_i}{\tau}$로 나누면 다음과 같습니다.
\[P(i) = \dfrac{e^{r_i / \tau}}{\sum e^{r_k / \tau}} = \dfrac{1}{1 + \underline{\sum_{k \neq i} e^{\frac{1}{\tau}(r_k - r_i)}} \cdots (*)} \label{eq2}\tag{2}\]- $\tau \to \infty$
- 이 경우 $(*) = 0$ 이 됩니다. 그러면 Eqn. 2에서 $P(i) = \frac{1}{k}$가 되므로 모든 슬롯머신을 동일한 확률로 무작위 탐색을 하게 됩니다.
- $\tau \to 0$
- 슬롯머신 $i$의 확률이 가장 높을 때
- $(*)$이 $0$으로 수렴하면서 $P(i) = 1$이 됩니다. 즉, 해당 슬롯머신만 계속 선택하게 됩니다.
- 다른 슬롯머신의 확률이 더 높을 때
- $(*) \to \infty$이므로 $P(i) = 0$이 됩니다. 해당 슬롯머신은 선택되지 않습니다.
- 슬롯머신 $i$의 확률이 가장 높을 때
Upper Confidence Bound (UCB)
지금까지의 알고리즘들은 모두 경험적으로 좋은 슬롯머신을 선택하고 특정 확률로 나머지 슬롯머신을 고르는 형태입니다. 하지만 슬롯머신에서 얻을 수 있는 보상은 상수가 아니라 특정 확률 분포에서 얻게 되는 확률 변수에 가깝습니다. 따라서 특정 슬롯머신에서 현재까지의 보상이 가장 좋다고 하더라도 실제로 그 슬롯머신이 최고의 선택은 아닐 수 있습니다.
Upper Confidence Bound (UCB)는 지금까지 가장 좋은 보상을 준 슬롯머신을 선택하면서 지금까지의 탐색 결과가 얼마나 확실한지 계산해 탐색 결과가 덜 확실한 슬롯머신을 더 탐색하는 방식입니다.
기본적인 틀은 다음 조건을 만족하는 슬롯머신 $i$를 찾는 것입니다.
\[i = \arg\max_i (\mu_i + P_i)\]$\mu_i$는 슬롯머신 $i$의 현재까지의 보상이며 $P_i$가 바로 Confidence bound가 됩니다. 이 $P_i$를 어떻게 정의하느냐에 따라 다른 알고리즘이 되며, UCB1, UCB2, UCB1-Normal 등 매우 다양한 방식이 있습니다. 본 포스트에서는 가장 단순한 UCB1에 대해서만 이야기 하도록 하겠습니다.
UCB1은 다음과 같이 정의합니다.
\[i = \arg\max_i \left( \bar{x}_i + \sqrt{\frac{2 \log t}{n_i}} \right) \label{eq3} \tag{3}\]- $\bar{x}_i$ : 슬롯머신 $i$에서 현재까지의 보상
- $t$ : 전체 슬롯머신 플레이 횟수 총합
- $n_i$ : 슬롯머신 $i$ 플레이 횟수
위 식은 Hoeffding’s Inequality를 통해 도출된다고 알려져 있습니다. 해당 내용은 본 포스트에서 다루지는 않겠습니다.
$\eqref{eq3}$ 에 따르면 UCB1 알고리즘은 처음엔 $t$가 작고 $n_i$도 작기 때문에 보상이 좋은 슬롯머신을 선택하면서 탐색이 덜 이루어진 슬롯머신을 선택하게 됩니다. ($t$는 log scale, $n_i$는 linear scale이기 때문입니다) 하지만 어느 정도 많은 탐색을 수행하였다면 현재까지의 보상에 더 비중을 둔 결과를 얻게 됩니다.
$\varepsilon$-greedy나 Softmax 보다는 더 좋은 퍼포먼스를 보여주는 알고리즘입니다. 단순히 랜덤 탐색을 하는 것이 아닌 근거 있는 선택을 한다는 점에서 왜 이 알고리즘이 어떤 슬롯머신을 선택했는지 유추할 수 있습니다. 하지만 UCB를 계산하기 위해서는 모든 슬롯머신에 대한 평균 보상을 알고 있어야 하므로 처음에 모든 슬롯머신을 다 탐색해야 한다는 문제가 있습니다.
Thompson Sampling
마지막으로 이론적으로나 실험적으로나 가장 좋은 퍼포먼스를 내는 알고리즘인 Thompson sampling에 대해서 알아보도록 하겠습니다.
Thompson sampling은 값을 직접 추정하기 보다는 사후 분포(Posterior)를 추정하여 해당 분포로부터 파라미터를 샘플링해 가장 높은 보상을 주는 슬롯머신을 작동하는 방식입니다. 이때 얻은 보상을 다시 베이즈 정리를 이용해서 분포를 업데이트합니다.
사후 분포는 다음과 같이 주어집니다.
\[P(\theta \mid D) \propto \prod P(r_i \mid a_i, \theta) P(\theta) \label{eq4} \tag{4}\]- $D = {(a_i, r_i) }$
- Parameter $\theta$
- Likelihood function $P(r \mid a, \theta)$
- Prior distribution $P(\theta)$
- 나중에 Conjugate prior를 이용하여 계산하게 됩니다.
여기서 Thompson sampling은 보상 기대치를 최대화할 확률이 높은 행동을 취하도록 구성되며, 행동 $a^\prime$은 다음 확률에 따라서 선택됩니다.
\[\int \mathbb{I} \left[ \mathbb{E}(r \mid a^*, \theta) = \max_{a^\prime} \mathbb{E}(r \mid a^\prime, \theta) \right] P(\theta \mid D) \; d\theta \label{eq5} \tag{5}\]실제로 사용할 때는 파라미터 $\theta^*$를 사후 분포 $P(\theta \mid D)$에서 샘플링하고, 다음의 샘플된 파라미터에 대한 보상 기댓값을 최대화하는 행동을 선택합니다.
\[a^\prime = \arg\max_a \mathbb{E}(r \mid a, \theta^*)\]Thompson sampling의 알고리즘은 다음과 같습니다.

여기서 각각의 슬롯머신이 Bernoulli distribution을 따른다고 가정하면 Conjugate prior를 이용해 간단하게 분포를 계산할 수 있습니다. Bernoulli distribution에 대한 Conjugate prior는 Beta distribution이기 때문에 $P(\theta)$를 Beta distribution으로 두고 계산합니다. 다시 말해서 파라미터 $\theta$를 Beta distribution에서 샘플링합니다.
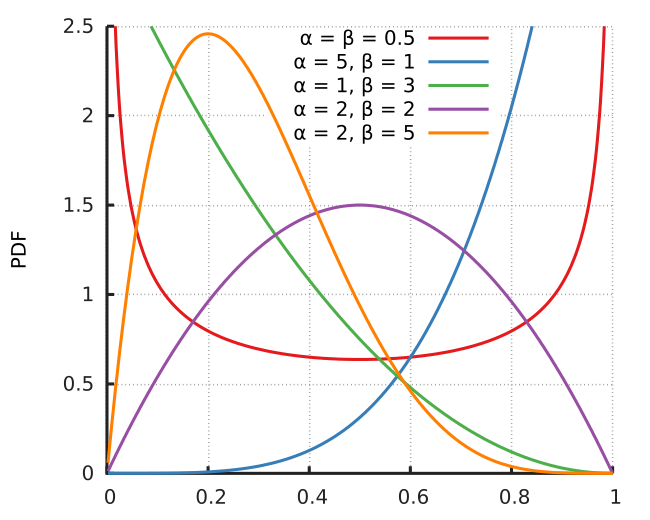
Beta distribution은 $\alpha$와 $\beta$ 두 파라미터를 두는데, 각각을 보상을 얻은 횟수, 보상을 얻지 못한 횟수로 두고 분포를 계산합니다. 위 이미지에서 알 수 있듯이 $\alpha » \beta$인 경우 1에 가까운 형태로 left-skewed 되는 것을 알 수 있습니다. 반대로 $\alpha « \beta$인 경우엔 0에 가깝게 right-skewed 되죠. 즉 보상을 얻은 횟수인 $\alpha$가 커질 수록 샘플링될 확률이 높아지게 됩니다. Beta distribution을 사용하는 Thompson sampling 알고리즘은 다음과 같습니다.

마무리
여기까지 Multi-armed bandit에 대해서 알아보았습니다. 네 개의 알고리즘의 퍼포먼스를 비교하면 일반적으로 다음과 같습니다.

Thompson sampling의 성능이 가장 좋고 UCB도 나쁘지 않은 퍼포먼스를 보입니다. 그러다보니 MAB를 다루는 대부분의 아티클이나 실제 구현체들도 Thompson sampling이 가장 많이 보입니다.
최근 MAB를 사용하는 케이스는 대외적으로 많이 알려져 있습니다. 카카오의 경우 MAB의 장점을 활용하여 추천 시스템을 운영하고 있고, NCSOFT 역시 MAB를 활용해 추천 시스템을 운영하고 있습니다.
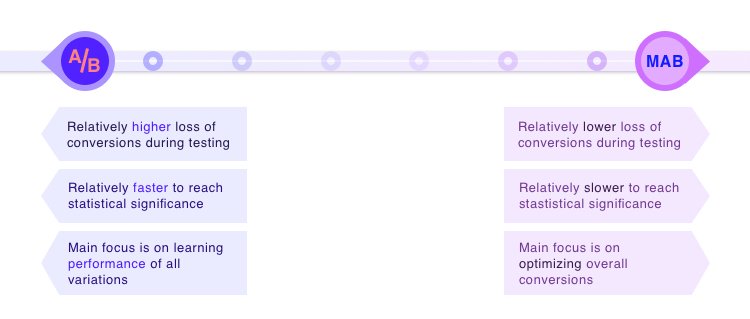
MAB가 A/B 테스트에 비해 많은 장점을 가지고는 있지만 상황에 따라서 잘 써야한다는 사실은 변하지 않습니다. 만약에 결과나 퍼포먼스에 대한 설명이 필요한 경우라면 MAB를 사용하는 것이 쉽지 않습니다. A/B 테스트의 경우 ‘통계적으로 유의미한 결과’를 보여줄 수 있지만 MAB는 그렇지 않기 때문이죠. 또한 MAB는 하나의 메트릭을 기준으로 최적화하게 됩니다. 따라서 여러 개의 메트릭을 동시에 바라보고 최적화하는 경우에도 A/B 테스트를 고민해야 합니다. 하지만 서비스의 트래픽이 적어 A/B 테스트가 어렵거나, 실시간성이 요구되는 경우, 그리고 퍼포먼스가 떨어지는 서비스를 제공하는 것이 비용적으로 큰 부담이 되는 경우에는 MAB를 사용하는 것이 올바른 선택입니다.
자세한 코드나 실험 자료는 이미 잘 설명된 아티클의 링크로 대신하여 포스트를 마무리하고자 합니다.
References
[5] A/B testing - Is there a better way? An exploration of multi-armed bandits
[7] https://webdocs.cs.ualberta.ca/~games/go/seminar/notes/2007/slides_ucb.pdf
[8] Chapelle, Olivier, and Lihong Li. “An empirical evaluation of thompson sampling.” Advances in neural information processing systems 24 (2011): 2249-2257.