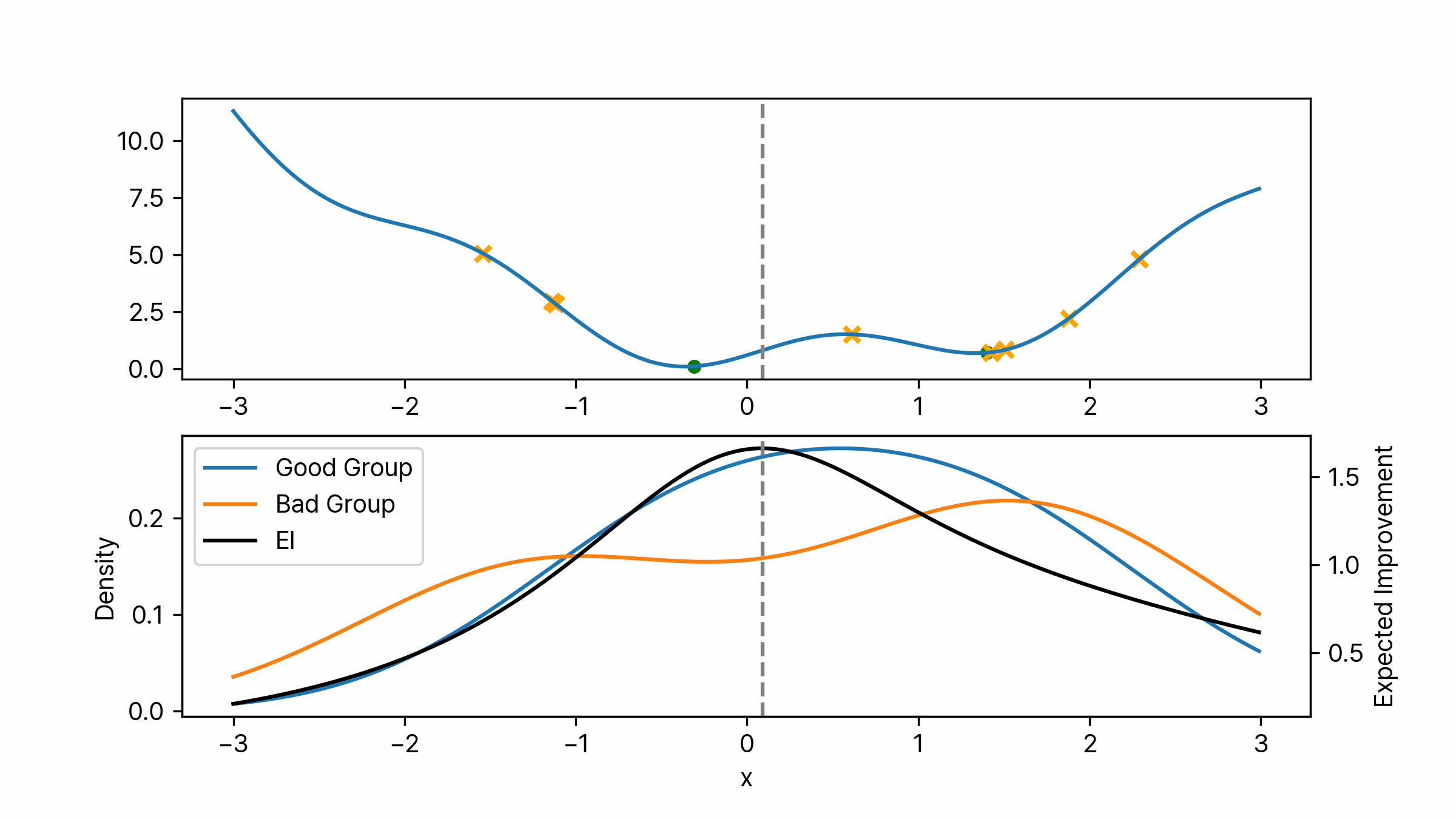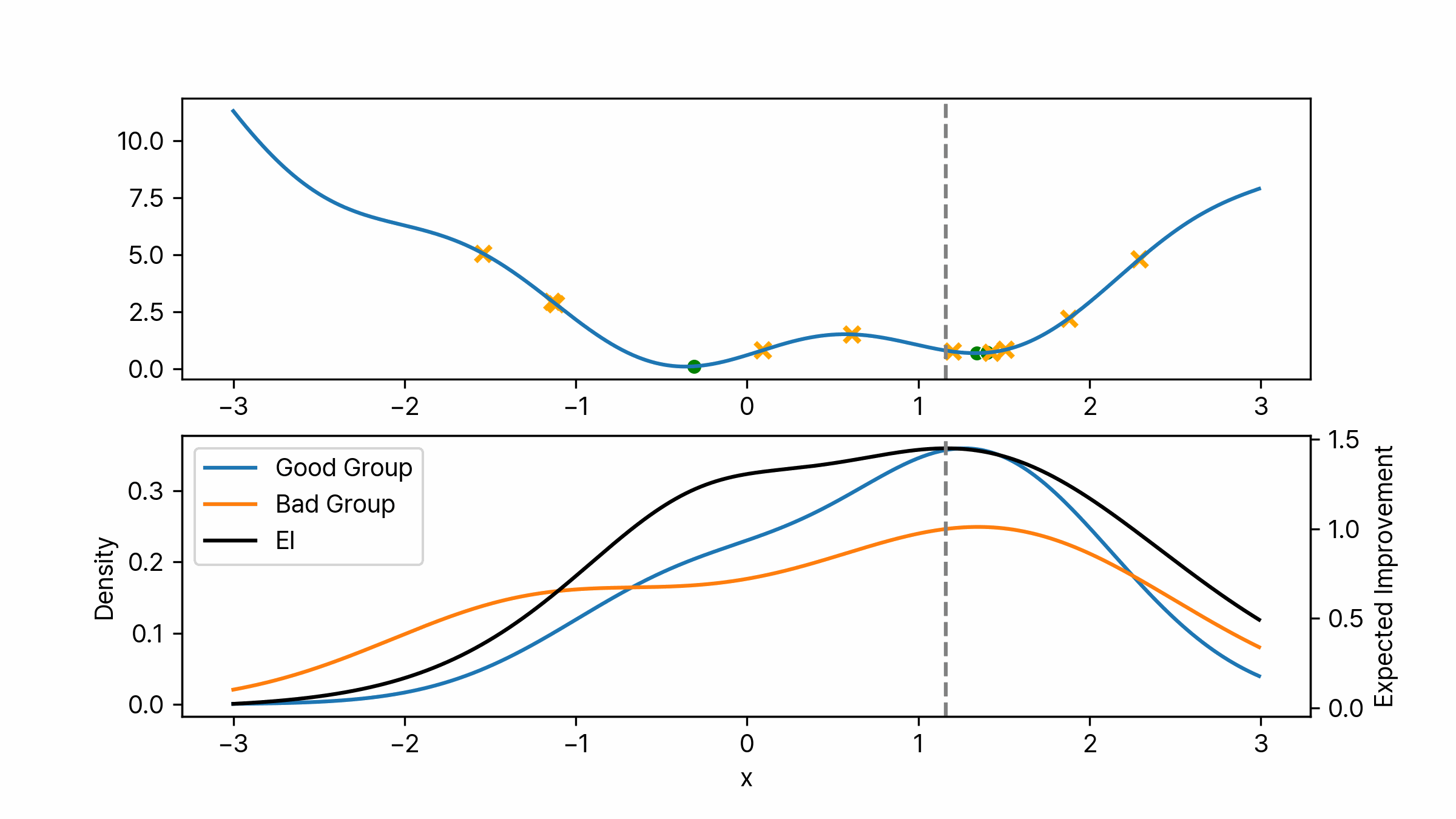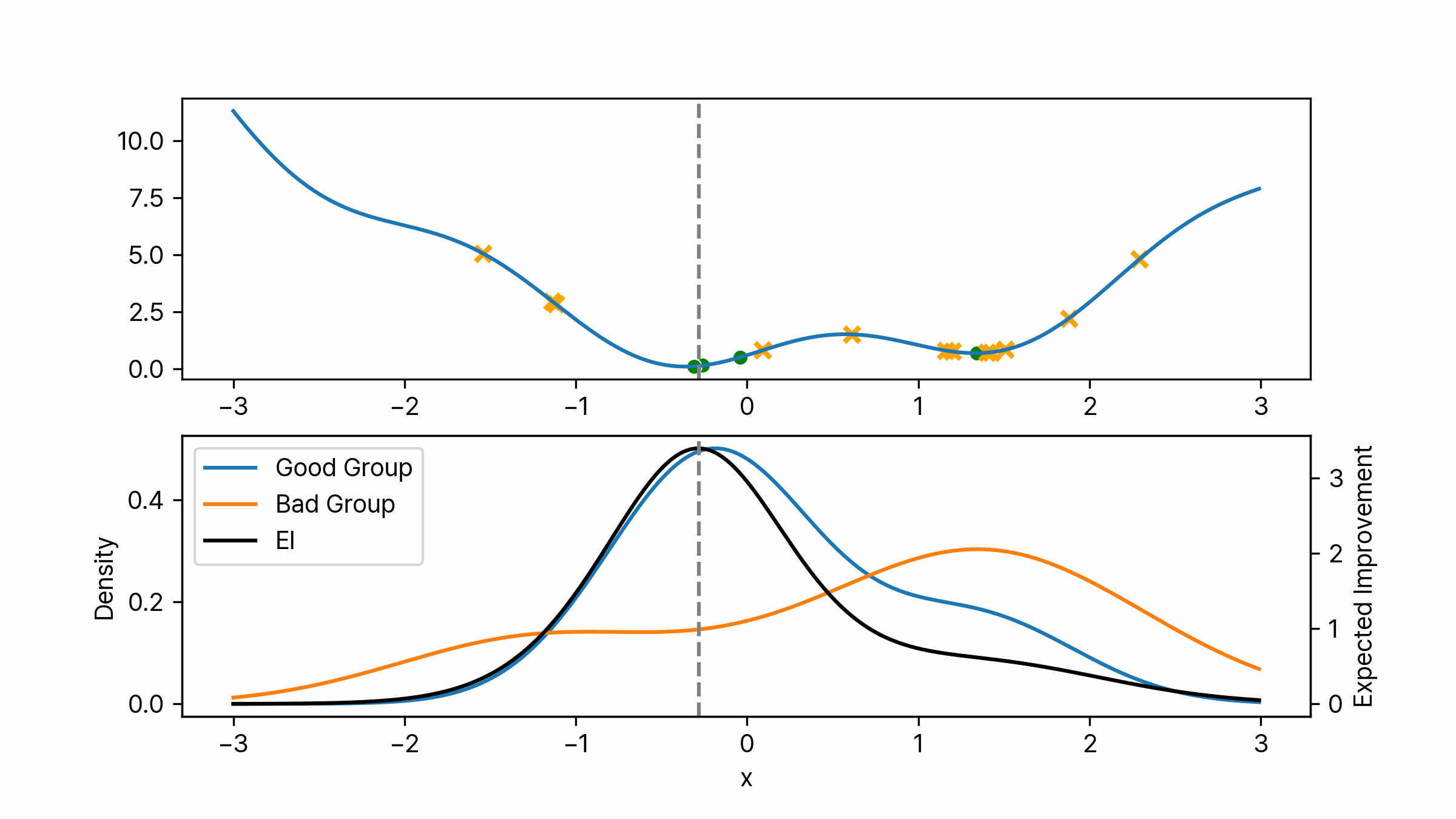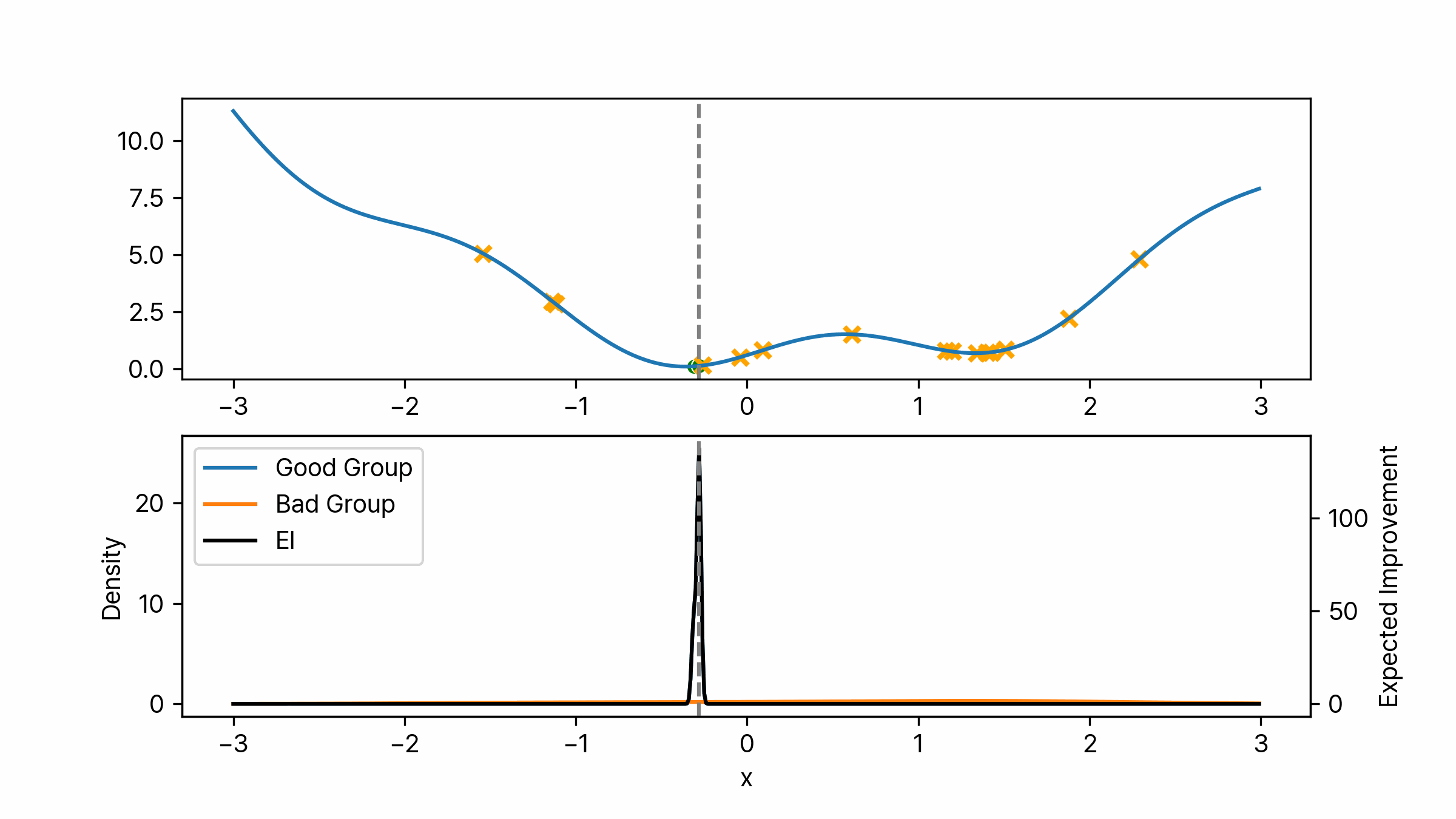Bayesian Optimization

들어가며

HPO 문제 정의

$N$ 개의 하이퍼 파라미터를 가진 머신러닝 알고리즘을 $\mathcal{A}$ 이라고 하겠습니다. 여러 개의 하이퍼파라미터 중 $n$ 번째의 하이퍼 파라미터를 $\Lambda_n$ 라고 한다면, 전체 하이퍼 파라미터 환경 공간 (hyperparameter configuration space) 는 다음과 같이 정의할 수 있습니다.

\[\boldsymbol{\Lambda} = \Lambda_1 \times \Lambda_2 \times \cdots \times \Lambda_N.\]

하이퍼 파라미터 벡터는 $\boldsymbol{\lambda} \in \boldsymbol{\Lambda}$ 로 적을 수 있고, 이 하이퍼 파라미터 벡터로 얻은 모델은 $\mathcal{A}_\lambda$ 로 둘 수 있습니다.

하이퍼 파라미터 튜닝은 주어진 학습 데이터, 검증 데이터에 대해서 손실 함수 (loss function)의 값을 최적으로 만드는 하이퍼 파라미터 $\boldsymbol{\lambda}^\ast$ 를 찾는 것이 목적입니다. 이를 주어진 데이터셋 $\mathcal{D}$ 에 대해 다음과 같이 쓸 수 있습니다.

\[\boldsymbol{\lambda^\ast} = \operatorname*{arg min}_{\boldsymbol{\lambda \in \boldsymbol{\Lambda}}} \ \mathbb{E}_{(D_{train}, D_{valid}) \sim \mathcal{D}} \mathbf{V}(\mathcal{L}, \mathcal{A}_\boldsymbol{\lambda}, D_{train}, D_{valid}).\]

$\mathbf{V}(\mathcal{L}, \mathcal{A}_\boldsymbol{\lambda}, D_{train}, D_{valid})$ 는 알고리즘 $\mathcal{A}$ 를 하이퍼 파라미터 $\boldsymbol{\lambda}$ 를 사용해 학습 데이터 $D_{train}$ 으로 학습하여 검증 데이터 $D_{valid}$로 평가한 손실 함수의 값을 얻는 것을 의미합니다. 검증 방법 $\mathbf{V}(\cdot, \cdot, \cdot, \cdot)$ 은 주어진 손실 함수에 대해 보통 홀드 아웃 (holdout)이나 교차 검증 (cross-validation)을 많이 사용합니다.

보다 간단한 설명을 위해 위 수식을 단순하게 생각한다면, 복잡한 블랙박스 함수 $f$ 에 대해서 그 값을 최소 또는 최대로 만들어주는 하이퍼 파라미터 $\boldsymbol{\lambda}$ 를 찾는 것으로 볼 수 있습니다.

\[\boldsymbol{\lambda}^\ast = \operatorname*{arg min}_{\boldsymbol{\lambda \in \boldsymbol{\Lambda}}} \ f(\boldsymbol{\lambda})\]

기존 블랙박스 하이퍼파라미터 최적화 방법

베이지안 최적화에 앞서 기존 블랙박스 방식의 최적화 방법은 크게 그리드 서치 (grid search)와 랜덤 서치 (random search)가 있습니다. 그리드 서치는 풀 팩토리얼 디자인 (full factorial design)이라고도 부르며, 각 하이퍼 파라미터 집합의 카르테시안 곱 (Cartesian product)을 하이퍼 파라미터 환경 공간으로 두는 방법입니다. 이 방법은 하이퍼 파라미터가 하나 추가 될 때마다 탐색해야 하는 공간이 커짐에 따라 차원의 저주 (the curse of dimensionality) 문제를 맞닥뜨리게 됩니다.

랜덤 서치는 이름에서 알 수 있듯이 정해진 횟수만큼 하이퍼 파라미터 환경 공간 내의 하이퍼 파라미터를 샘플링하여 탐색하는 방법입니다. 이 방법은 몇몇 하이퍼 파라미터가 다른 하이퍼 파라미터에 비해 더 중요한 경우 좋은 성능을 보인다고 합니다.

Comparison between Grid Search and Random Search

또한 그리드 서치에 비해 병렬화가 쉽고 자원 할당이 보다 유연하다는 장점을 갖고 있습니다. 랜덤 서치는 머신러닝 알고리즘에 대한 가정을 하지 않은 채로 최적화하고, 충분한 자원이 주어진다면 최적 성능에 근접한 성능을 보인다는 점에서 유용한 베이스라인이 됩니다.

베이지안 최적화 (Bayesian Optimization)

베이지안 최적화는 블랙박스 모델에 대한 전역 최적화를 위한 가장 최신의 방법론입니다. 최근 다양한 분야의 머신러닝 모델에서 매우 좋은 결과를 보여주고 있으며, 꾸준히 연구도 진행 중이기도 합니다.

베이지안 최적화를 의사 코드 (Pseudo-code)로 나타내면 다음과 같습니다.

Bayesian Optimization Pseudocode

앞으로 자세히 설명할 내용을 배제하고 설명을 해보겠습니다. 우선 블랙박스 함수 $f$는 모델에서 사용하는 손실 함수로 생각하면 편합니다. 우선 하이퍼 파라미터와 그 하이퍼 파라미터로 얻을 모델에 대한 $f$의 값을 저장할 집합 $\mathcal{H}$를 초기화합니다. 그리고 어떤 값을 탐색해야 할지 계산하는 함수인 획득 함수를 통해 하이퍼 파라미터 후보를 찾습니다. 그 후보값을 이용해 $f$ 의 값을 계산하여 $\mathcal{H}$ 에 저장합니다. 그리고 지금까지 얻은 관측 결과를 복잡한 함수 $f$ 대신 계산할 대체 모델에 적합시킵니다. 그리고 이 과정을 계속 반복합니다.

사실 이런 내용은 HyperOpt나 Optuna와 같은 툴이 대신 해주기 때문에 큰 흐름만 파악해도 문제가 없다고 생각합니다. 하지만 베이지안 최적화에서 중심이 되는 두 가지 요소는 반드시 자세하기 짚고 넘어가야 합니다. 바로 획득 함수와 대체 모델입니다.

획득 함수 (Acquisition function)

획득 함수의 역할은 가장 적절한 다음 하이퍼 파라미터 후보를 찾아주는 것입니다. 직관적으로 생각했을 때 가장 적절한 다음 후보는 지금까지 가장 좋았던 결과의 근처에 있거나 지금까지 탐색하지 않은 알 수 없는 곳에 있을 수 있습니다. 서로 트레이드오프(trade-off) 관계에 있는 이 두 경우를 각각 착취(Exploitation)와 탐색(Exploration)이라고 하는데요. 획득 함수는 이 두 가지를 잘 조율하여 최적의 하이퍼 파라미터 후보를 찾습니다.

주로 Improvement 기반의 획득 함수, UCB와 같은 Confidence bound 기반의 획득 함수 등이 있는데 본 글에서는 가장 자주 쓰이는 Improvement 기반의 획득 함수에 대해서 다루고자 합니다.

Probability of Improvement (PI)

가장 먼저 소개할 획득 함수는 Probability of Improvement (PI) 입니다. PI는 의미 그대로, 블랙박스 함수 $f$에 대해서 지금까지 최적의 하이퍼 파라미터인 $\boldsymbol{\lambda}^\ast$보다 더 좋은 성능을 내는 하이퍼 파라미터에 대한 확률을 통해서 다음 후보를 찾는 방법입니다.

\[\boldsymbol{\lambda}^+ = \operatorname*{arg max}_{\boldsymbol{\lambda}} \ PI(\boldsymbol{\lambda}) = \operatorname*{arg max}_{\boldsymbol{\lambda}} \ P(f(\boldsymbol{\lambda}) \le f(\boldsymbol{\lambda}^\ast)).\]

개념은 간단하지만 이 방법은 근본적으로 탐색보다는 착취에 초점을 맞추고 있습니다. 이미 얻은 최적의 하이퍼 파라미터 근처의 하이퍼 파라미터만을 후보로 반환하는 경우가 발생합니다. 이렇게 되면 최초 몇 번의 시행에서 어떤 하이퍼 파라미터를 먼저 찾았느냐에 따라 편향된 최적화 결과를 얻을 수 있습니다. 따라서 착취와 탐색의 트레이드오프를 조절할 수 있는 하나의 파라미터를 추가하여 문제를 완화할 수 있습니다.

\[\boldsymbol{\lambda}^+ = \operatorname*{arg max}_{\boldsymbol{\lambda}} \ P(f(\boldsymbol{\lambda}) \le f(\boldsymbol{\lambda}^\ast) - \varepsilon).\]

물론 파라미터 $\varepsilon \geq 0$ 를 따로 설정해야 하는 점이 단점이 되기도 합니다. $\varepsilon$의 값이 너무 크거나 너무 작아도 문제가 되는데요. 만약 $\varepsilon$이 0에 가까울만큼 작다면 기존의 PI와 차이가 없는 착취에 초점을 맞춘 결과를 얻게 됩니다. 하지만 $\varepsilon$이 너무 크다면 어떤 하이퍼 파라미터라도 PI가 높게 나올 수 있기 때문에 탐색만 수행하는 결과를 얻을 수도 있습니다. Agnihotri & Batra, “Exploring Bayesian Optimization”, Distill, 2020.에서 $\varepsilon$의 변화에 따른 PI가 어떻게 변하는지 확인할 수 있습니다.

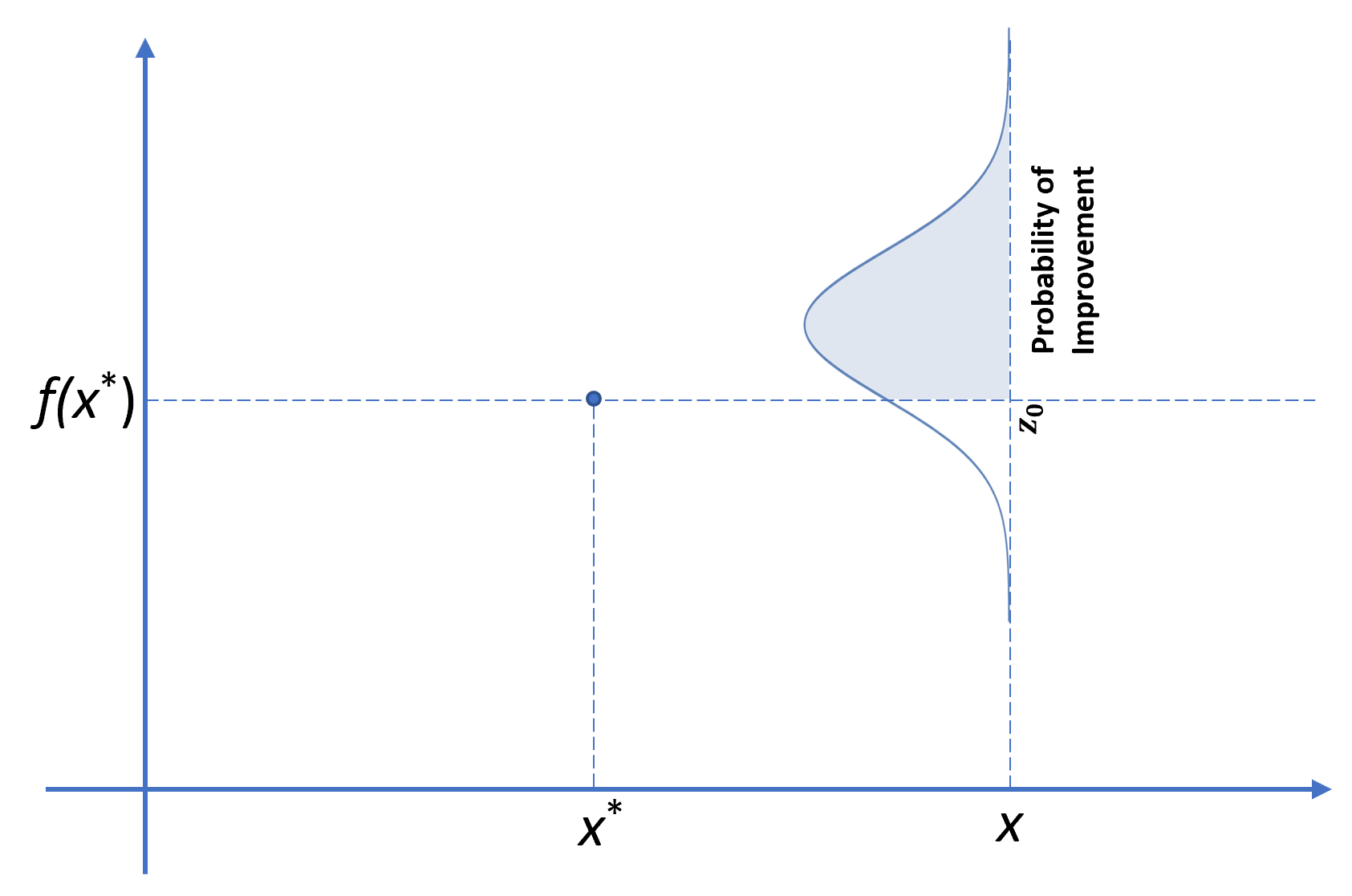Probability of Improvement Function

Expected Improvement (EI)

PI는 현재 최적의 하이퍼 파라미터를 기준으로 결과가 개선될 확률만을 보기 때문에 실제로 어느 정도의 개선이 이루어지는지는 고려하지 않습니다. 따라서 어떤 하이퍼 파라미터를 통해 $f$의 값에 대해 큰 개선이 이루어지더라도 그 확률이 낮다면 고려하지 않는거죠. 결국 착취와 탐색의 트레이드오프에서 탐색의 비중이 너무 낮습니다. 이러한 PI의 아쉬운 점을 해결하기 위해 개선 확률이 아닌 얼마나 개선할 수 있는지에 초점을 맞추는 새로운 방법이 등장합니다. 바로 Expected Improvement (EI) 입니다. $f(\boldsymbol{\lambda}^\ast)$ 관점에서 더 개선할 수 있는 정도의 기댓값을 최대화하는 다음 후보를 찾는 방식입니다.

\[\boldsymbol{\lambda}^+ = \operatorname*{arg max}_{\boldsymbol{\lambda}} \ EI(\boldsymbol{\lambda}) = \operatorname*{arg max}_{\boldsymbol{\lambda}} \ \mathbb{E}[\max(0, f(\boldsymbol{\lambda}^\ast) - f(\boldsymbol{\lambda})) \mid \mathcal{D}]\]

식에서도 알 수 있듯이 후보 하이퍼 파라미터의 함수값이 기존보다 좋아지지 못할 경우엔 0으로 설정하여 그 기댓값을 계산하도록 합니다. 위 식에서 $y = f(\boldsymbol{\lambda})$ 로 둔 다음 EI를 적분 식으로 나타내면 다음과 같습니다.

\[EI(\boldsymbol{\lambda}) = \int_{-\infty}^\infty \max(0, f(\boldsymbol{\lambda}^\ast) - y) \cdot p(y \mid \boldsymbol{\lambda}) \ dy.\]

여기서 $p(y \mid \boldsymbol{\lambda})$ 는 추후 다룰 대체 모델의 확률 분포입니다.

EI는 지금까지 탐색된 최적의 하이퍼 파라미터 근처 뿐만 아니라 적절한 탐색을 통해 PI에서 발생하는 문제를 완화하였습니다. 실무적인 관점에서도 PI보다 나은 성능을 보이는 경우가 많아 베이지안 최적화에서 가장 많이 쓰이는 획득 함수입니다. PI에 비해 성능이 잘 나오는 이유를 살펴보자면 모델의 손실 함수의 형태는 일반적인 함수에 비해 많은 Local minima를 갖기 때문입니다. PI를 사용한다면 몇 번의 시도에서 얻은 최적의 하이퍼 파라미터 근처에서 최적화 결과를 얻게 되어 쉽게 Local minima에 빠지는 문제가 발생할 수 있지만, EI를 이용하면 PI에 비해 탐색의 비중이 높기 때문에 아까와 같은 문제가 덜 발생하게 됩니다. 이는 자연스레 성능의 향상을 기대할 수 있게 됩니다.

대체 모델 (Surrogate Models)

대체 모델의 정의는 목적 함수(objective function)에 대한 확률적 표현이자 모델입니다. 조금 더 풀어쓰자면 복잡한 목적 함수가 어떻게 생겼는지 알 수 없으므로 지금까지 나온 결과들을 통해 목적 함수를 완벽하게는 아니더라도 이를 대체할 수 있을 정도로 확률적인 표현을 하는 모델입니다. 따라서 베이지안 최적화를 많이 수행하였다면 지금까지 나온 결과가 충분히 많을 것이고, 대체 모델은 목적 함수에 매우 근사한 형태를 띄게 됩니다. 하지만 우리는 목적 함수의 완벽한 형태가 필요한 것이 아니라 최소점 또는 최대점 근처의 형태만 알면 되고, 그 근처의 값들은 위에서 다룬 획득 함수를 통해 선정됩니다.

본 글에서는 전통적인 Gaussian Process와 2011년 “Algorithms for Hyper-parameter Optimization” 논문에서 다뤄진 이후 지금 가장 많이 쓰이는 Tree-structred Parzen Estimators를 다루고자 합니다.

Gaussian Process

베이지안 최적화에 있어서 가우시안 프로세스(Gaussian Process, GP)는 전통적으로 많이 사용하였던 대체 모델입니다. 가우시안 프로세스의 표현력, 스무스함, 신뢰구간 추정, 예측 분포에 대한 닫힌 형태 (closed form)의 계산 가능성 같은 다양한 이유 때문인데요.

가우시안 프로세스 $\mathcal{G}(m(\boldsymbol{\lambda}), k(\boldsymbol{\lambda}, \boldsymbol{\lambda}^\prime))$는 평균 함수 $m(\boldsymbol{\lambda})$, 공분산 함수 $k(\boldsymbol{\lambda}, \boldsymbol{\lambda}^\prime)$을 이용하여 표현합니다. 베이지안 최적화에서 평균 함수는 보통 상수로 가정합니다. 노이즈가 없다는 가정 하에 평균과 분산에 대한 예측 $\mu(\cdot)$과 $\sigma^2(\cdot)$은 다음과 같습니다.

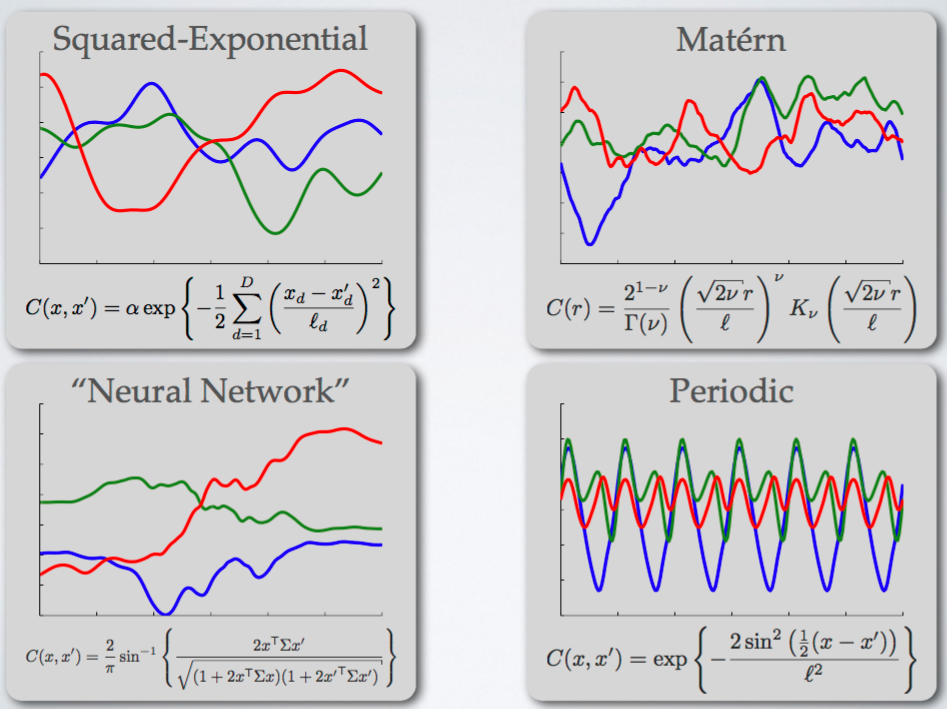
\[\mu(\boldsymbol{\lambda}) = \mathbf{k}^T_\ast \mathbf{K}^{-1} \mathbf{y}, \quad \sigma^2(\boldsymbol{\lambda}) = k(\boldsymbol{\lambda, \boldsymbol{\lambda}}) - \mathbf{k}^T_\ast \mathbf{K}^{-1} \mathbf{k}_\ast\]

여기서 $\mathbf{k}_\ast$는 $\boldsymbol{\lambda}$와 지금까지의 관측값 사이의 공분산 벡터를 의미하며, $\mathbf{K}$는 지금까지 계산된 하이퍼 파라미터 설정들의 공분산 행렬, $\mathbf{y}$는 관측된 함수값입니다. 가우시안 프로세스는 공분산 함수가 성능의 대부분을 결정 짓는데요. 일반적으로는 Mátern 5/2 Kernel을 사용합니다. Squared Exponential Kernel 같은 함수도 존재하지만 복잡한 함수를 표현하기엔 너무 평탄(smooth)한 함수여서 실제 함수를 제대로 표현하기 어렵다는 문제가 있습니다.

GP Kernels

Mátern 5/2 Kernel은 조금 복잡하지만 다음과 같습니다.

\[K_{M52}(x, x^\prime) = \theta_0 \left( 1 + \sqrt{5r^2(x, x^\prime)} + \frac{5}{3}r^2 (x, x^\prime) \right) \exp \left\{ - \sqrt{5r^2 (x, x^\prime)} \right\}.\] \[r^2(x, x^\prime) = \sum^D_{d=1} \frac{(x_d - x_d^\prime)^2}{\theta_d^2}.\]

가우시안 프로세스의 가장 큰 단점은 너무나 큰 계산량입니다. 가우시안 프로세스는 데이터 포인트의 수 $n$에 대해서 $O(n^3)$의 계산 복잡도를 가집니다. 다른 연산보다도 행렬 $\mathbf{K}$의 Inverse와 Determinant를 계산하는 것에 많은 시간이 필요합니다. 따라서 큰 데이터에 대해서는 가우시안 프로세스를 사용하기 어려워집니다. 보다 유연하고 확장성 높은 대체 모델을 찾는 연구는 계속 되었고, 앞으로 설명할 것이 위 문제들을 어느 정도 해결함에 따라 최근 가장 많이 사용되는 대체 함수인 Tree-structured Parzen Estimator입니다.

Tree-structured Parzen Estimators (TPE)

TPE와 가우시안 프로세스의 가장 큰 차이는 어떤 것을 모델링하는가에 있습니다. 가우시안 프로세스는 어떤 하이퍼 파라미터에 대해 어떤 목적 함수 값이 나오는가를 모델링합니다. 조건부 확률로 나타낸다면 $p(y \mid \boldsymbol{\lambda})$를 모델링합니다. 하지만 TPE는 $p(\boldsymbol{\lambda} \mid y )$를 모델링합니다. 주어진 목적 함수의 값에 대해서 하이퍼 파라미터의 확률 분포를 모델링하는거죠.

TPE의 첫 단계는 최초 몇 번의 시행을 통해 목적 함수 값들을 얻어 알고리즘을 초기화하는 것입니다. 그 다음 얻은 결과를 목적 함수 값을 기준으로 두 분포로 나눕니다. 기준이 되는 임계값 $y^\ast$가 있다고 할 때, $p(\boldsymbol{\lambda} \mid y)$는 다음과 같이 나눌 수 있습니다.

\[p(\boldsymbol{\lambda} \mid y) = \begin{cases} \ell(\boldsymbol{\lambda}) \quad \text{if } y < y^\ast \\ g(\boldsymbol{\lambda}) \quad \text{if } y \ge y^\ast \end{cases}\]

$\ell(\boldsymbol{\lambda})$는 목적 함수의 값이 임계값보다 낮은, 즉 성능이 좋은 하이퍼 파라미터에 대한 분포가 됩니다. 반대로 $g(\boldsymbol{\lambda})$는 낮은 성능을 보이는 하이퍼 파라미터들의 분포가 됩니다. 이 때 분포를 생성할 때 Parzen Estimator를 사용하는데요. 이름은 생소하지만 우리가 자주 사용하는 Kernel Density Estimator와 동일합니다. 일반적인 Gaussian KDE를 통해서 분포를 생성할 수 있습니다. 마지막으로 임계값을 설정하는 방법이 중요한데, 어떤 분위수(Quantile) $\gamma$를 통해 임계값을 설정합니다.

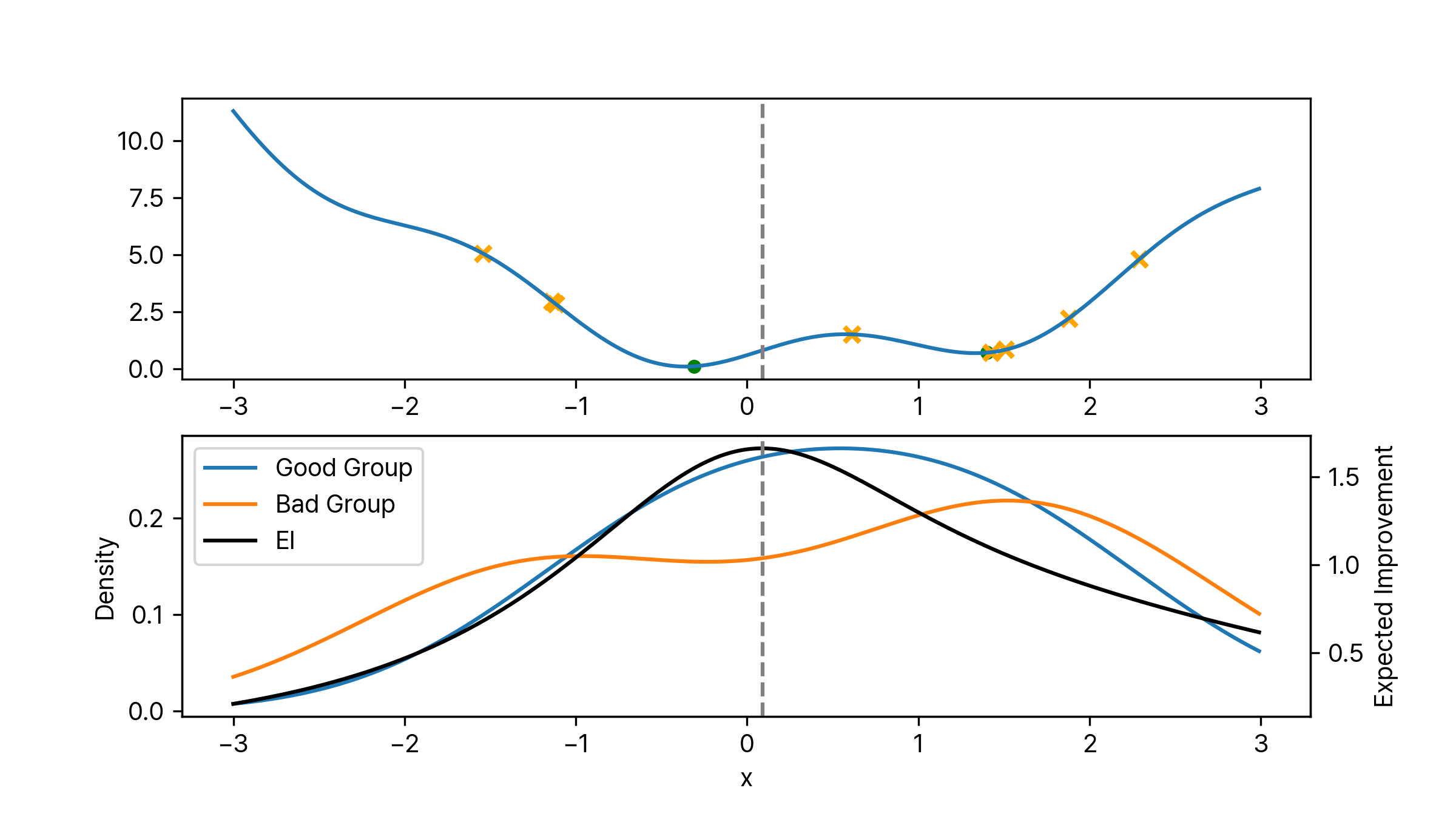
\[p(y < y^\ast) = \gamma\]

일반적으로 $\gamma$는 0.15나 0.2 정도의 값으로 설정합니다. 만약 $\gamma$를 0.2로 설정하고 최초 열 번의 시행을 통해 알고리즘을 초기화했다면 $\ell(\boldsymbol{\lambda})$는 두 개의 결과로 분포가 생성이 됩니다. $g(\boldsymbol{\lambda})$는 여덟 개의 값으로 분포가 생성 되겠죠. 아래 이미지는 어떤 함수에 대해서 위 설정대로 초기화를 한 결과입니다. 노란색 X는 $g(\boldsymbol{\lambda})$에 포함되는 포인트이며 초록색 점은 $\ell(\boldsymbol{\lambda})$에 포함되는 포인트입니다. 각각의 분포는 위에서 언급한 것과 같이 Gaussian KDE를 통해 생성하였습니다. 그럼 여기서 다음 탐색을 위한 하이퍼 파라미터 후보는 어떻게 찾을 수 있을까요? 위에서 계속 다루어 왔듯이 베이지안 최적화에서는 이럴 때 획득 함수를 이용합니다. $p(y \mid \boldsymbol{\lambda})$에 대해 Expected Improvement를 계산하면 됩니다.

Expected Improvement

TPE 알고리즘에서 EI 최적화하기

아까 EI의 정의를 다시 확인해보겠습니다.

\[EI(\boldsymbol{\lambda}) = \int_{-\infty}^\infty \max(0, f(\boldsymbol{\lambda}^\ast) - y) \cdot p(y \mid \boldsymbol{\lambda}) \ dy.\]

이 식을 조금 더 간단하게 만들 수 있습니다. 우선 편의를 위해 $y^\ast = f(\boldsymbol{\lambda}^\ast)$로 두겠습니다. 이때 $y$가 $y^\ast$보다 큰 경우, 즉 최적 성능보다 좋지 않은 경우에는 적분 값이 0이 됩니다. 위 식은 $y$가 $y^\ast$보다 작을 때만 의미가 있습니다. 따라서 $y$에 대해 $y^\ast$ 까지만 적분한 것과 $\infty$까지 적분한 것이 같아지죠. 그래서 위 식은 다음과 같이 쓸 수 있습니다.

\[EI(\boldsymbol{\lambda}) = \int_{-\infty}^\infty \max(0, y^\ast - y) \cdot p(y \mid \boldsymbol{\lambda}) \ dy = \int_{-\infty}^{y^\ast} (y^\ast - y) \cdot p(y \mid \boldsymbol{\lambda}) \ dy.\]

위 적분 식을 조금 더 정리해야 하는데요. 베이즈 정리(Bayes’ Theorem)를 사용하면 됩니다. 베이즈 정리에 의해 $p(y \mid \boldsymbol{\lambda}) = \frac{p(\boldsymbol{\lambda} \mid y) p(y)}{p(\boldsymbol{\lambda})}$이기 때문에 위 식은 다음과 같이 쓸 수 있습니다.

\[EI(\boldsymbol{\lambda}) = \int_{-\infty}^{y^\ast} (y^\ast - y) \cdot p(y \mid \boldsymbol{\lambda}) \ dy = \int_{-\infty}^{y^\ast} (y^\ast - y) \cdot \frac{p(\boldsymbol{\lambda} \mid y) p(y)}{p(\boldsymbol{\lambda})} \ dy.\]

우리는 위에서 분위수를 $\gamma = p(y < y^\ast)$로 정의하였으며, $p(\boldsymbol{\lambda})$는 Marginalization을 통해 다음과 같이 쓸 수 있습니다.

\[\begin{aligned} p(\boldsymbol{\lambda}) &= \int_\mathbb{R} p(\boldsymbol{\lambda} \mid y) p(y) dy \\ &= \int_{-\infty}^{y^\ast} p(\boldsymbol{\lambda} \mid y) p(y) dy + \int_{y^\ast}^\infty p(\boldsymbol{\lambda} \mid y) p(y) dy \\ &= \gamma \ell(\boldsymbol{\lambda}) + (1- \gamma) g(\boldsymbol{\lambda}). \end{aligned}\]

이제 $\int_{-\infty}^{y^\ast} (y^\ast - y) \cdot p(\boldsymbol{\lambda} \mid y)p(y) dy$만 정리하면 되는데, 이 역시 위와 비슷한 방법으로 계산할 수 있습니다.

\[\begin{aligned} \int_{-\infty}^{y^\ast} (y^\ast - y) \cdot p(\boldsymbol{\lambda} \mid y)p(y) \; dy &= \ell(\boldsymbol{\lambda}) \int_{-\infty}^{y^\ast} (y^\ast - y) \cdot p(y) \; dy\\ \\ &= \ell(\boldsymbol{\lambda}) \int_{-\infty}^{y^\ast} y^\ast p(y) - y p(y) \; dy \\ &= \ell(\boldsymbol{\lambda}) \gamma y^\ast - \ell(\boldsymbol{\lambda}) \int_{-\infty}^{y^\ast} y p(y) \; dy \\ &= \ell(\boldsymbol{\lambda}) \gamma y^\ast - \ell(\boldsymbol{\lambda}) A \end{aligned}\]

지금까지의 결과로 EI 식을 정리하면 다음과 같습니다.

\[\begin{aligned} EI(\boldsymbol{\lambda}) &= \int_{-\infty}^{y^\ast} (y^\ast - y) \cdot \frac{p(\boldsymbol{\lambda} \mid y) p(y)}{p(\boldsymbol{\lambda})} \ dy \\ &= \frac{\ell(\boldsymbol{\lambda}) \gamma y^\ast - \ell(\boldsymbol{\lambda}) A}{\gamma \ell(\boldsymbol{\lambda}) + (1- \gamma) g(\boldsymbol{\lambda})} \\ &= \frac{\gamma y^\ast - A}{\gamma + (1-\gamma) \frac{g(\boldsymbol{\lambda})}{\ell(\boldsymbol{\lambda})}} \\ & = C \cdot \left( \gamma + \frac{g(\boldsymbol{\lambda})}{\ell(\boldsymbol{\lambda})} (1-\gamma) \right)^{-1} \qquad \text{where } C = \gamma y^\ast - A \\ &\propto \left( \gamma + \frac{g(\boldsymbol{\lambda})}{\ell(\boldsymbol{\lambda})} (1-\gamma) \right)^{-1} \end{aligned}\]

마지막 식을 통해 TPE에서 최대의 EI를 갖는 하이퍼 파라미터 $\boldsymbol{\lambda}$는 $\ell(\boldsymbol{\lambda})$ 분포에서 높은 확률을 가지면서 동시에 $g(\boldsymbol{\lambda})$에선 낮은 확률을 가져야 함을 알 수 있습니다. 쉽게 설명하자면 성능이 낮은 그룹의 분포의 확률 대비 성능이 높은 그룹의 분포의 확률이 높은 하이퍼 파라미터가 다음 후보가 됩니다. 실제 구현에서는 간단하게 $\frac{\ell}{g}$가 가장 큰 하이퍼 파라미터를 반환하도록 합니다. 아래 이미지는 위 과정을 애니메이션으로 나타낸 것입니다. 몇 번의 시행이 지나면 특정 포인트로 수렴하는 것을 볼 수 있습니다.

TPE

레퍼런스

[1] https://distill.pub/2020/bayesian-optimization/

[2] https://medium.com/criteo-engineering/hyper-parameter-optimization-algorithms-2fe447525903

[3] https://towardsdatascience.com/bayesian-optimization-concept-explained-in-layman-terms-1d2bcdeaf12f